DFT-1/2 和 DFT-PPS 密度泛函方法计算电子态
版本:2017.0
QuantumATK 的2017年版本为计算半导体和绝缘体的电子结构引入了两个新颖的密度泛函修正方法:DFT-1/2 和赝势投影偏移(DFT-PPS)法。本教程将介绍如何使用这些方法。
DFT-1/2 通常也被称为 LDA-1/2 或 GGA-1/2,它是一种半经验方法,用于校正扩展系统的局部和半局部交换关联密度函数中自相互作用误差,在精神上类似于 DFT + U 法。因此,可以将其视为具有大致相同目标的 TB09-Meta-GGA 法的替代方法,改进了导带能级和带隙的描述。与 TB09-MGGA 一样,DFT + 1/2 方法不适用于依赖总能量和力的计算,例如几何优化。
PPS 是赝势投影偏移的缩写。本着 Zunger 和他的同事在 [WZ95] 中提出经验赝势的精神,这种方法在 SG15 赝势中引入了非局部投影的经验偏移。调整投影的偏移是为了重现半导体技术上的重要属性,例如带隙和晶格常数。PPS 法目前可直接用于元素硅和锗,但也可通过手动设置适当的投影偏移(必须首先确定这些)用于其他元素。重要的是,PPS 法确实适用于半导体材料结构的几何优化。
DFT-1/2 法
DFT-1/2法试图通过定义一个原子自能势抵消电子-空穴自相互能以修正 DFT 的自相互作用误差。为系统中的原子位点计算该电势,并将其定义为中性原子电势与移除它一部分电荷(介于0和1个电子之间)之后产生离子的电势之差。总的自能势是这些原子势的总和。文献 [FMT11] 中的研究已经发现在 DFT 哈密顿量基础上增加 DFT-1/2 自能势可以大幅度地增加多种半导体和绝缘系统的带隙。更多相关信息,请参阅 QuantumATK 手册条目 DFT-1/2 法。
重要
该方法并非完全没有经验参数,例如使用的截断半径。依据参考文献 [FMT08] 和 [FMT11],选择截断半径以使带隙最大化。
还要注意的是,并非系统中的所有元素都必须进行 DFT-1/2 校正。通常建议仅将其添加到阴离子物质中,而使阳离子物质保持正常。
QuantumATK 中提供了默认的 DFT-1/2 参数;并已针对各种材料进行了优化,且在大多数情况下,相对于标准的 LDA 或 GGA 改进了带隙。
采用 PBE-1/2 的 InP 能带结构
创建一个新的 QuantumATK 项目(最好放在一个新文件夹中),打开 ![]() Builder,然后点击 Add
Builder,然后点击 Add ![]() From Database,选择数据库中的 InP 晶体。
From Database,选择数据库中的 InP 晶体。
将 InP 晶体添加到 Builder 的 Stash,然后把构型发送到 ![]() Script Generator。之后添加以下脚本模块:
Script Generator。之后添加以下脚本模块:
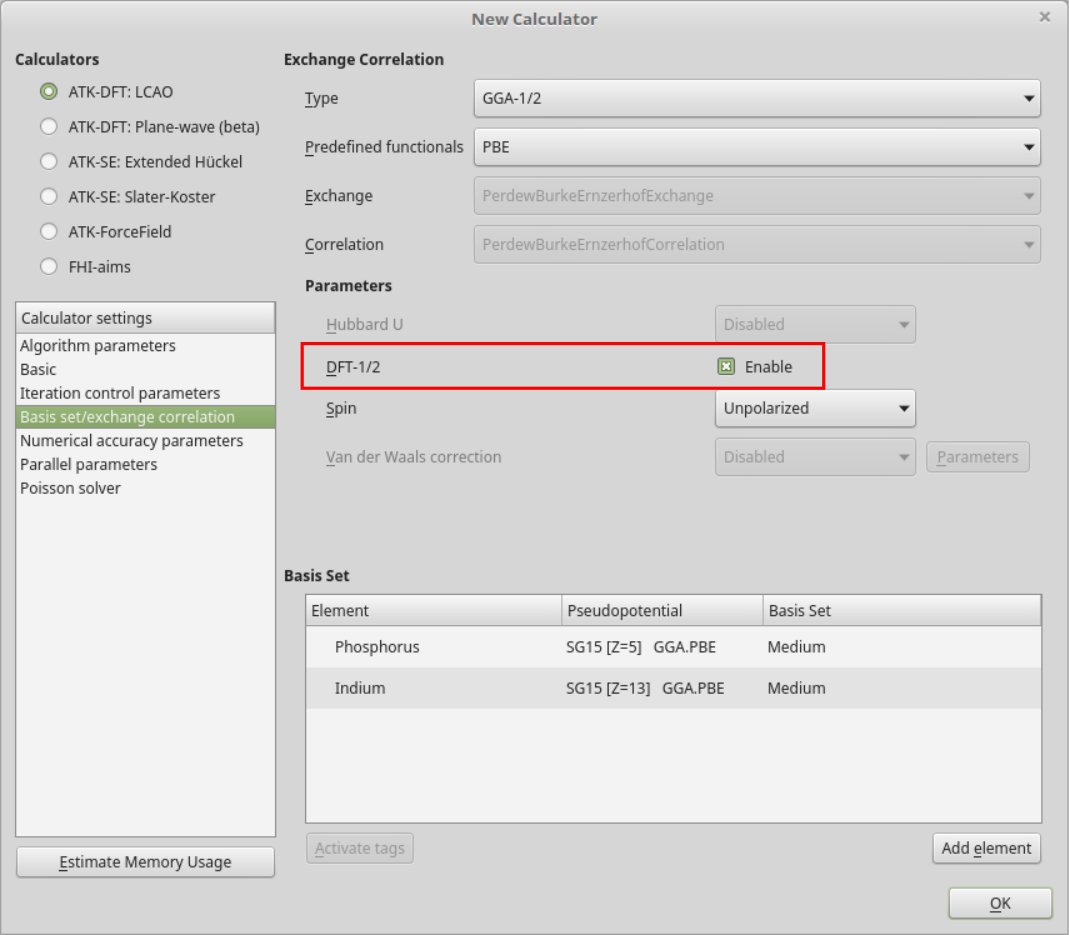
打开计算器界面调整计算器参数。
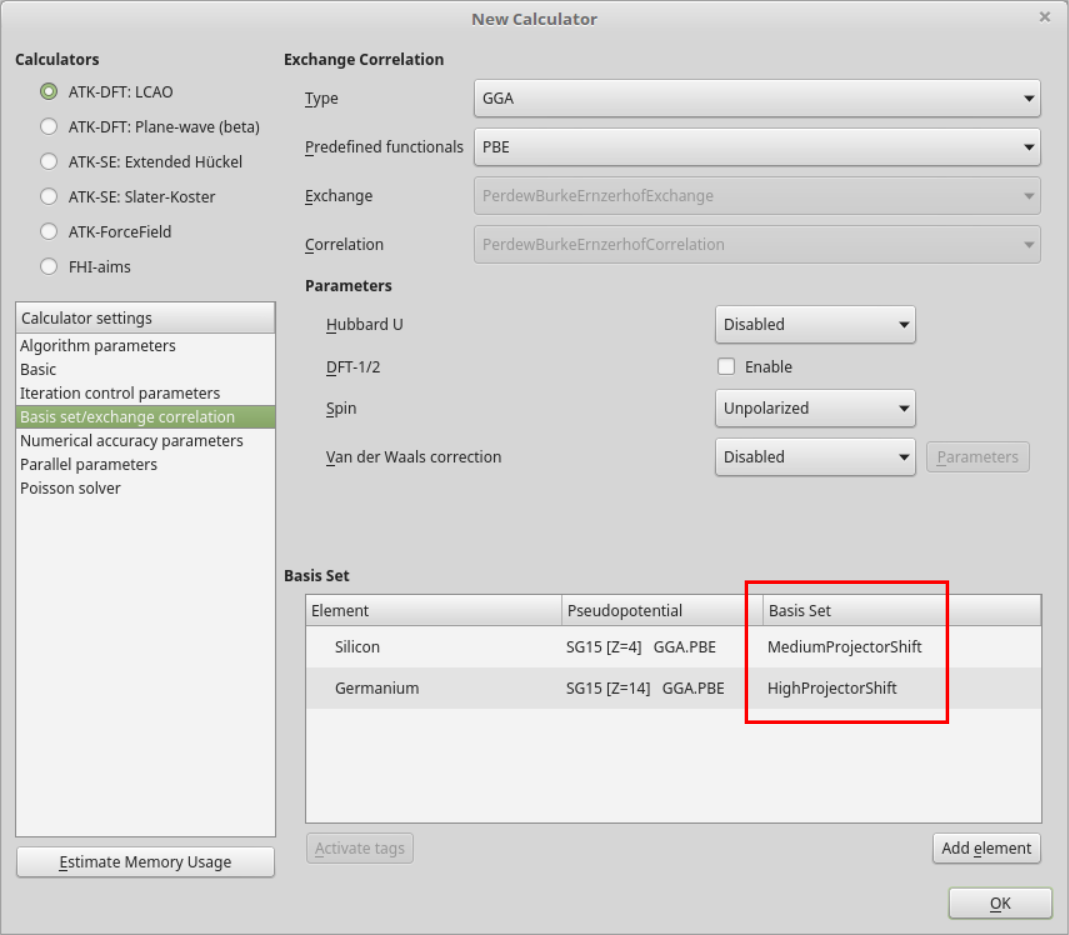
k 点网格选择 9x9x9,点击 Basis set/exchange correlation,注意默认的交换关联方法是 “GGA”(PBE)。如下图勾选 DFT-1/2 处 Enable 前的选项框。
关闭计算器的界面,保存脚本为 InP.py。如果您利用 ![]() Editor 打开脚本,将会看到交换关联方法是
Editor 打开脚本,将会看到交换关联方法是 GAHalf.PBE:
#---------------------------------------- # Exchange-Correlation #---------------------------------------- exchange_correlation = GGAHalf.PBE
即采用 PBE 函数的 GGA-1/2,也可称为 PBE-1/2。如有需要,你可在此处下载脚本:↓ InP.py。
或从终端运行:
$ atkpython InP.py > InP.log
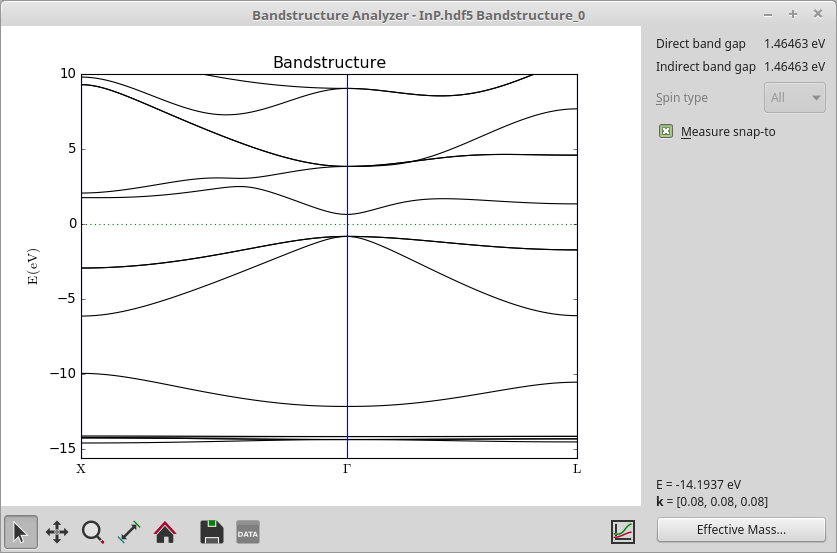
本次计算将会非常快。结束后利用 Bandstructure Analyze 绘制出产生的能带结构。您将发现 InP 是一个直接带隙半导体,带隙值为 1.46 eV,与文献 [LRS96] 中的实验带隙 1.34 eV 很接近。
提示
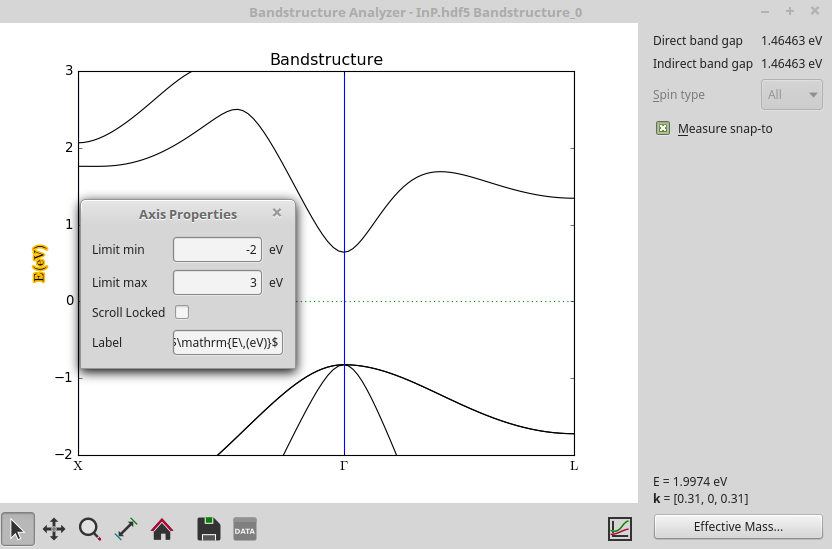
为看得更清楚,您也许想要放大费米能级周围的能带。这里有两种方法实现:
- 利用 Zoom 工具(从左数的第三个图标)
- 或点击 y 轴的标记并选中,然后右击并选择 Edit item 打开 Axis Properties 界面,您可以在这里调整 y 轴的范围。
III-V 型半导体的带隙
下图显示了 DFT-1/2 法(LDA-1/2 和 GGA-1/2)与采用默认赝势和基组的 LDA、GGA、TB09-MGGA 标准带隙计算的比较。所有计算中采用的 k 点网格均为 9x9x9,实验带隙数据来自文献 [LRS96]。
很明显,DFT-1/2 的校正可以改进标准的 LDA 和 GGA 带隙,这些间隙通常很小或不存在(没有呈柱状显示)。自洽的 TB09-MGGA 计算确定的 c 参数通常也可以提高带隙。
采用 LDA-1/2 和 GGA-1/2 计算 Ge 的红条表示错误地预测了直接带隙(如在实验中用 $\Gamma$-$\Gamma$ 代替 $\Gamma$-L)。使用 GGA-1/2 计算 GaP 的橙色条表示正确地预测了该带隙是间接的,但是错误地预测了 L 处凹谷的能带比 X 处凹谷的能带低。
手动设置 DFT-1/2 参数
当然,我们可以不使用默认参数,而是手动地设置 DFT-1/2 的参数。这可以通过创建 DFTHalfParameters 类的实例来实现,然后将其作为基组的参数。
让我们以 GaAs 为例。以下脚本手动地将 As 的 DFT-1/2参数设置为与默认参数相同,并使 Ga 的 DFT-1/2 校正禁用,这也是默认行为。请注意基组的 dft_half_parameters 参数:
#---------------------------------------- # Basis Set #---------------------------------------- # LDA-1/2 parameters for As dft_half_parameters = DFTHalfParameters( element=Arsenic, fractional_charge=[0.3, 0.0], cutoff_radius=4.0*Bohr, ) # No LDA-1/2 parameters are needed for Ga (Disabled) basis_set = [ LDABasis.Arsenic_DoubleZetaPolarized( dft_half_parameters=dft_half_parameters), LDABasis.Gallium_DoubleZetaPolarized( dft_half_parameters=Disabled), ]
更多信息,请参见 QuantumATK 手册的 Input format for DFT-1/2 和 DFT-1/2 default parameters 部分。
警告
在确定默认参数已格外注意的情况下,选择适当的 DFT-1/2 参数仍可能是一件非常棘手的事情。如果您选择使用非默认的 DFT-1/2 参数,则这些参数的质量将完全由用户自己承担!
QuantumWise 不支持确定自定义 DFT-1/2 参数。我们一般建议用户坚持使用默认值。
DFT-PPS 法
如上文所述,DFT-PPS 法是将偏移应用于 SG15 赝势的非局域投影。赝势的非局域部分 $\hat{V}_\text{nl}$ 根据以下修改:
$$\hat{V}_\text{nl} \rightarrow \hat{V}_\text{nl} \mathrel{+} \sum_l |p_{l} \rangle \alpha_{l} \langle p_{l} | ,$$
求和覆盖了所有的投影 $p_{l}$,$\alpha_{l}$ 是一个取决于轨道角动量量子数 $l$ 的经验参数。注意,这种方法不会增加 DFT 计算的计算成本!
所需的投影偏移参数已针对硅和锗进行了优化,仅可与 PBE 密度函数和 SG15 赝势一起使用。这些作为单独的基组实现:
BasisGGASG15.Silicon_LowProjectorShift BasisGGASG15.Silicon_MediumProjectorShift BasisGGASG15.Silicon_HighProjectorShift BasisGGASG15.Silicon_UltraProjectorShift BasisGGASG15.Germanium_MediumProjectorShift BasisGGASG15.Germanium_HighProjectorShift BasisGGASG15.Germanium_UltraProjectorShift
对于每一种元素,同样的优化投影偏移设置都应用在所有的 SG15 基组。脚本 ↓ projector_shifts.py 展示了 Si 和 Ge 的固有 DFT-PPS 参数。
basis_sets = [ BasisGGASG15.Silicon_MediumProjectorShift, # Si PPS-PBE SG15-Medium BasisGGASG15.Germanium_HighProjectorShift , # Ge PPS-PBE SG15-High ] for basis_set,element in zip(basis_sets,['Si','Ge']): print(element) projector_shift = basis_set.projectorShift() print("s-shift: %+.3f eV" % projector_shift.sOrbitalShift().inUnitsOf(eV)) print("p-shift: %+.3f eV" % projector_shift.pOrbitalShift().inUnitsOf(eV)) print("d-shift: %+.3f eV" % projector_shift.dOrbitalShift().inUnitsOf(eV))
运行后会产生如下所示的输出。Si 的 d-shift 是 0.0 eV,因为硅没有 d 电子:
Si s-shift: +21.330 eV p-shift: -1.430 eV d-shift: +0.000 eV Ge s-shift: +13.790 eV p-shift: +0.220 eV d-shift: -2.030 eV
Si、SiGe、Ge 的带隙和晶格常数
如下所示,在 ![]() Script Generator 中,通过为 Si 或 Ge 选择其中一个
Script Generator 中,通过为 Si 或 Ge 选择其中一个 ProjectorShift 基组就可以启动 DFT-PPS 法。从普通 PBE 切换到 DFT-PPS 无需更改其他计算器设置。
DFT-PPS 法非常方便的一点是,它可以像普通 GGA 计算一样进行几何优化(力和应力最小化)–实际上,通常选择 DFT-PPS 参数提供高度精确半导体晶格常数的同时还能得到准确的带隙。
接下来,您将研究块体 Si 和 Ge 和一个简单的 50/50 SiGe 合金。这三个块体构型在脚本 ↓ bulks.py 中定义。脚本 ↓ pbe.py 运行对 3 个构型进行结构优化和能带结构分析,而 ↓ pps.py 采用 DFT-PPS 法进行同样的操作。
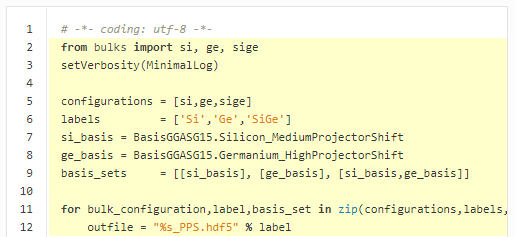
最后一个脚本如下所示。请注意该特定脚本中从第 2 到 12 行,从外部脚本导入了块体构型,并在这些构型和基组上建立了 Python 循环:
1 # -*- coding: utf-8 -*- 2 from bulks import si, ge, sige 3 setVerbosity(MinimalLog) 4 5 configurations = [si,ge,sige] 6 labels = ['Si','Ge','SiGe'] 7 si_basis = BasisGGASG15.Silicon_MediumProjectorShift 8 ge_basis = BasisGGASG15.Germanium_HighProjectorShift 9 basis_sets = [[si_basis], [ge_basis], [si_basis,ge_basis]] 10 11 for bulk_configuration,label,basis_set in zip(configurations,labels,basis_sets): 12 outfile = "%s_PPS.hdf5" % label 13 14 # ------------------------------------------------------------- 15 # Calculator 16 # ------------------------------------------------------------- 17 k_point_sampling = MonkhorstPackGrid( 18 na=9, 19 nb=9, 20 nc=9, 21 ) 22 numerical_accuracy_parameters = NumericalAccuracyParameters( 23 k_point_sampling=k_point_sampling, 24 density_mesh_cutoff=90.0*Hartree, 25 ) 26 27 calculator = LCAOCalculator( 28 basis_set=basis_set, 29 numerical_accuracy_parameters=numerical_accuracy_parameters, 30 ) 31 32 bulk_configuration.setCalculator(calculator) 33 nlprint(bulk_configuration) 34 bulk_configuration.update() 35 nlsave(outfile, bulk_configuration) 36 37 # ------------------------------------------------------------- 38 # Optimize Geometry 39 # ------------------------------------------------------------- 40 fix_atom_indices_0 = [0, 1] 41 constraints = [FixAtomConstraints(fix_atom_indices_0)] 42 43 bulk_configuration = OptimizeGeometry( 44 bulk_configuration, 45 max_forces=0.05*eV/Ang, 46 max_stress=0.1*GPa, 47 max_steps=200, 48 max_step_length=0.2*Ang, 49 constraints=constraints, 50 trajectory_filename=None, 51 optimizer_method=LBFGS(), 52 constrain_bravais_lattice=True, 53 ) 54 nlsave(outfile, bulk_configuration) 55 nlprint(bulk_configuration) 56 57 # ------------------------------------------------------------- 58 # Bandstructure 59 # ------------------------------------------------------------- 60 bandstructure = Bandstructure( 61 configuration=bulk_configuration, 62 route=['L', 'G', 'X'], 63 points_per_segment=50 64 ) 65 nlsave(outfile, bandstructure)
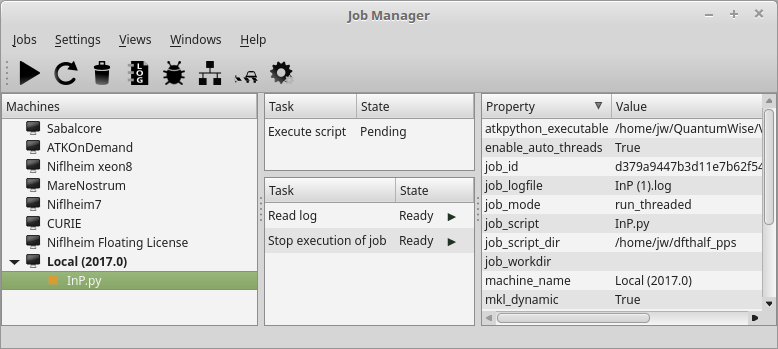
下载这 3 个脚本(↓ bulks.py, ↓ pbe.py, ↓ pps.py),用 ![]() Job Manager 或从终端运行后两个脚本:
Job Manager 或从终端运行后两个脚本:
$ atkpython pps.py > pps.log $ atkpython pbe.py > pbe.log
每个作业执行大概需要 5 分钟。
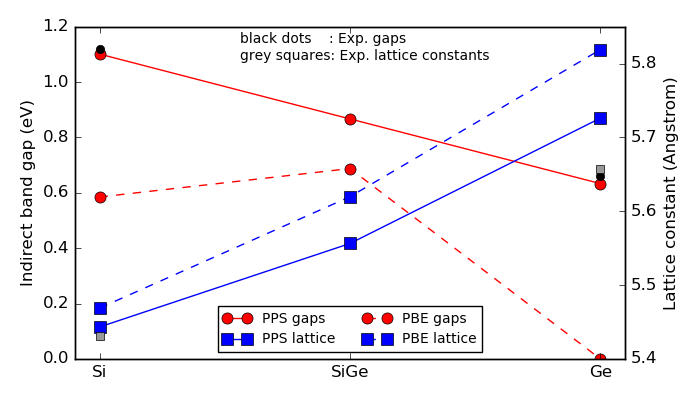
然后使用脚本 ↓ plot_pps.py 绘制结果。运行该脚本应产生下图,其中对于 PBE (虚线)和 DFT-PPS (实线),计算出的间接带隙显示为红色圆圈,计算出的晶格常数显示为蓝色正方形。
Si 和 Ge 的 DFT-PPS 带隙与实验比较一致(黑色圆点;来自参考文献 [LRS96] ),并且随锗含量递增大致呈线性变化。相反地,普通的 PBE 法预测 Ge 带隙为零。
与未经校正的 PBE 相比,纯 Si 和 Ge 的 DFT-PPS 晶格常数也更接近实验(灰色方块)。
手动设置 DFT-PPS 参数
当然,也可以手动设置 DFT-PPS 投影偏移参数,而不使用默认值。对于没有默认 DFT-PPS 参数(仅 Si 和 Ge 当前具有默认值)的元素,这将在 DFT-PPS 计算中特别有用。
PseudoPotentialProjectorShift 类的一个实例提供投影偏移,然后将其作为 SG15 基组的参数。例如,以下脚本手动地将 Si 和 Ge 的 DFT-PPS 参数设置为默认:
#---------------------------------------- # Basis Set #---------------------------------------- # Basis set for Silicon SiliconBasis_projector_shift = PseudoPotentialProjectorShift( s_orbital_shift=21.33*eV, p_orbital_shift=-1.43*eV, d_orbital_shift=0.0*eV, f_orbital_shift=0.0*eV, g_orbital_shift=0.0*eV ) SiliconBasis = BasisGGASG15.Silicon_Medium(projector_shift=SiliconBasis_projector_shift) # Basis set for Germanium GermaniumBasis_projector_shift = PseudoPotentialProjectorShift( s_orbital_shift=13.79*eV, p_orbital_shift=0.22*eV, d_orbital_shift=-2.03*eV, f_orbital_shift=0.0*eV, g_orbital_shift=0.0*eV ) GermaniumBasis = BasisGGASG15.Germanium_High(projector_shift=GermaniumBasis_projector_shift) # Total basis set basis_set = [ SiliconBasis, GermaniumBasis, ]
警告
选择适当的 DFT-PPS 参数可能是一件非常微妙的事情,并且通常需要数值优化程序。SciPy 软件可以提供许多此类例程,但是,如果您选择使用非默认 DFT-PPS 参数,则这些参数的质量完全由用户自己承担!
QuantumWise 不支持优化 DFT-PPS 参数。如果有默认参数的,我们通常建议用户使用默认值。
参考
- [FMT08] Luiz G. Ferreira, Marcelo Marques, and Lara K. Teles. Approximation to density functional theory for the calculation of band gaps of semiconductors. Phys. Rev. B, 78:125116, Sep 2008. doi:10.1103/PhysRevB.78.125116.
- [FMT11] (1, 2) Luiz G. Ferreira, Marcelo Marques, and Lara K. Teles. Slater half-occupation technique revisited: the LDA-1/2 and GGA-1/2 approaches for atomic ionization energies and band gaps in semiconductors. AIP Adv., 1(3):032119, 2011. doi:10.1063/1.3624562.
- [LRS96] (1, 2, 3) M. Levinshtein, S. Rumyantsev, and M. Shur, editors. Handbook Series on Semiconductor Parameters. volume 1. World Scientific Publishing Cp. Pte. Ltd., Singapore, 1996.
- [WZ95] L.-W. Wang and A. Zunger. Local-density-derived semiempirical pseudopotentials. Phys. Rev. B, 51:17398–17416, 1995. doi:10.1103/PhysRevB.51.17398.