电极化
铁电 BaTiO3 的自发极化
介绍
铁电(FE)材料具有自发电极化的特性,可以通过施加外部电场实现逆转。FE 材料可应用于电容器、铁电随机存取存储器(RAM),最近在铁电隧道结(FTJ)中展示出巨电阻效应[1] [2]。
研究最多的 FE 材料之一是钛酸钡(BaTiO3),也就是本教程的主题。在继续计算之前,让我们先简要总结一些核心理论概念。
电极化的现代理论
FE 材料的理论认识由所谓的电极化现代理论来描述[3]。通常将材料的极化分成电子和离子两部分。后者可以使用简单的经典静电点电荷求和计算获得。
$$\mathbf{P}_i = \frac{|e|}{\Omega}\sum_\nu Z^\nu_\mathrm{ion} \mathbf{r}^\nu,$$
$Z^\nu_\mathrm{ion}$ 和 $\mathbf{r}^\nu$ 是原子 $\nu$ 的价电荷和位置矢量,$\Omega$ 为单胞体积,求和范围为单胞里的所有离子。
电子对电极化的贡献可从如下公式得到[3]:
$$\mathbf{P}_e = -\frac{2|e|i}{(2\pi)^3}\int_A d\mathbf{k}_\bot\sum_{n=1}^M\int_0^{G_\parallel}\langle u_{\mathbf{k},n}| \frac{\partial}{\partial k_\parallel}|u_{\mathbf{k},n}\rangle dk_\parallel,$$
这里的求和范围为所有的占据能带,$k_\parallel$ 平行于极化方向,$G_\parallel$ 为相同方向上的倒易晶格矢量。$|u_{\mathbf{k},n}\rangle$ 态为Bloch 函数的晶胞周期性部分,$\psi_{\mathbf{k},n}(\mathbf{r}) = u_{n,\mathbf{k}}(\mathbf{r})e^{i\mathbf{k}\cdot\mathbf{r}}$。最后一个积分被称为贝利相位。 垂直方向上的积分易与几个 k 点交叉。而平行方向上的 k 点数量应该更大。
总的电极化为简单地电子贡献部分和离子贡献部分的加和,
$$\mathbf{P}_t = \mathbf{P}_i + \mathbf{P}_e.$$
参考文献[3]中的一个重要发现为电极化是一个多值函数,而实际上形成了一个晶格。原因在于电子极化 $\mathbf{P}_e$ 是由对 $2\pi$ 取模计算得到的贝利相位确定的。同样地,如果所有的离子在任一方向上被晶格常数取代,离子贡献部分 $\mathbf{P}_i$ 就会得到一个不同的值。
因此,电极化是一个周期函数,周期称为极化量子,$\mathbf{P}_q^j=\frac{|e|\mathbf{R}^j}{\Omega}$,$e$ 是电子电荷,$\mathbf{R}^j$ 是指晶格矢量 $j$,$\Omega$ 为单胞体积。
鉴于极化的多值性,只有极化差异也许并不奇怪,两个不同结构之间的 $\Delta \mathbf{P}$ 是具有明确性的。
ATK 分别计算和报告电子贡献部分和离子贡献部分,还有极化量子。
重要
注意,该操作对于金属系统不起作用,并且在可能的情况下应该优选正交晶胞。在 2D 系统和非正交单元中使用时应彻底地测试使用的设置和结果。
铁电 BaTiO3 的自发极化
提示
本教程使用特定版本的QuantumATK创建,因此涉及的截图和脚本参数可能与您实际使用的版本略有区别,请在学习时务必注意。
- 不同版本的QuantumATK的py脚本可能不兼容;
- 较新的版本输出的数据文件默认为hdf5;
- 老版本的数据文件为nc文件,可以被新版本读取。
BaTiO3 的晶体结构
钛酸钡(BaTiO3)室温下为四方晶体结构,单胞在 c 方向上略微伸长。内应力进一步使 c 方向上的分数坐标偏离其高对称位置。在本教程中,我们使用从 Inorganic Crystal Structure Database (ICSD)中获得的实验晶格常数和坐标。以下 QuantumATK 格式给出的结构如下[4]
# Set up lattice lattice = SimpleTetragonal(3.9945*Angstrom, 4.0335*Angstrom) # Define elements elements = [Barium, Titanium, Oxygen, Oxygen, Oxygen] # Define coordinates fractional_coordinates = [[ 0. , 0. , 0. ], [ 0.5 , 0.5 , 0.51427 ], [ 0.5 , 0.5 , 0.974477], [ 0.5 , 0. , 0.487618], [ 0. , 0.5 , 0.487618]] # Set up configuration bulk_configuration = BulkConfiguration( bravais_lattice=lattice, elements=elements, fractional_coordinates=fractional_coordinates )
计算设置
在本节,您将为计算 BaTiO3 晶体电极化设置采用 局域密度近似(LDA)的 DFT 计算。您将使用 QuantumATK 进行计算,建议先参阅 QuantumATK tutorial 熟悉基本工作流程。
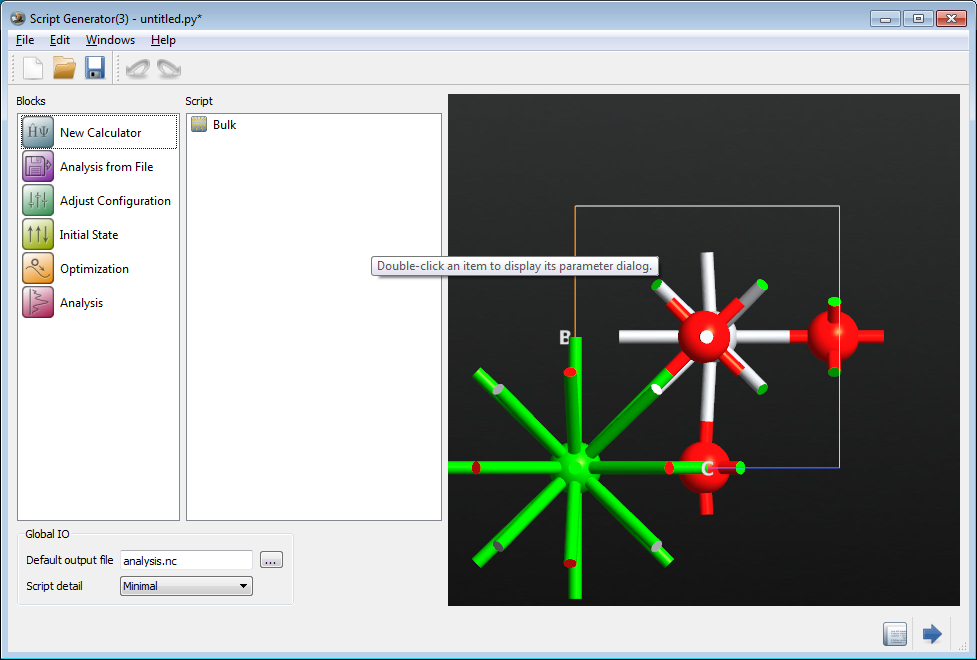
启动 QuantumATK,为本例创建一个新项目,用一个新的空目录。选择上面 python 脚本中的 BaTiO3 结构文本并拖拽到 Script Generator 按钮 ![]() 上。该工具将解译脚本并打开导入的结构。
上。该工具将解译脚本并打开导入的结构。
提示
或者,您可以将脚本保存到项目目录中,然后将文件从 QuantumATK 主窗口拖放 Script Generator。
接下来的步骤如下:
- 更改默认输出文件为
BaTiO3_lda.nc。
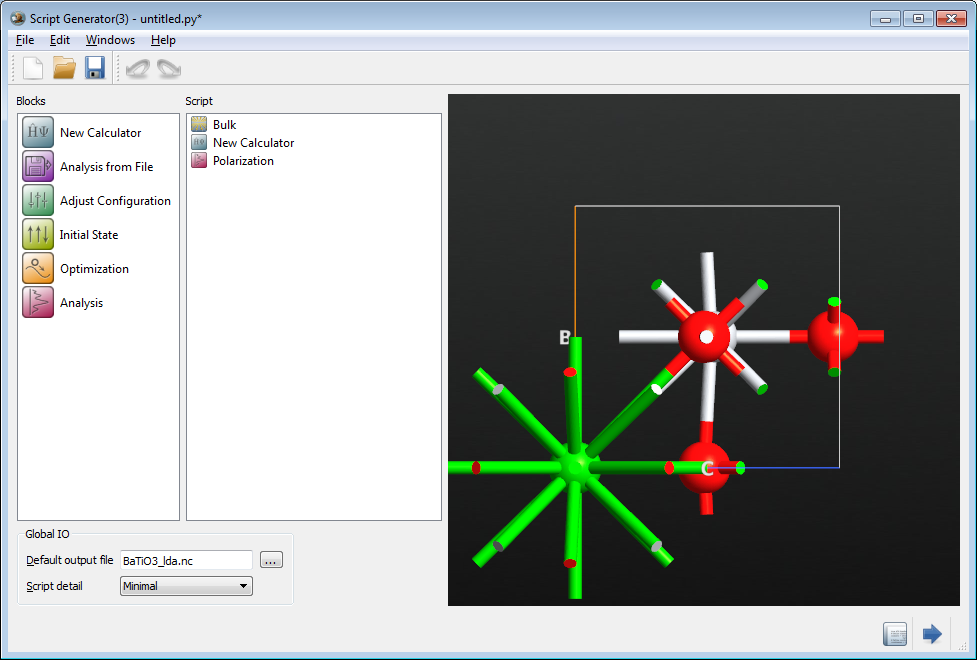
现在双击“Script”面板上的 New Calculator 模块打开计算器窗口。
设置 k 点取样为 5×5×5,其他选项按照默认设置就可以了。
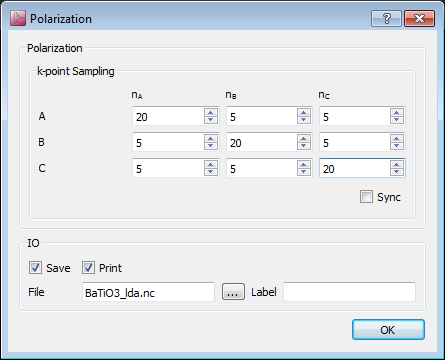
下一步要为极化分析调整参数。双击 Polarization 模块。
将对角线上的 k 点数目增加到 20。这是沿着积分线的k点数,需要相对较高。您应该始终通过比较具有不同k点数的计算来检验收敛。其他的 k 点值取 5 对应于横向 k 点数目以用于在布里渊区平均。相对于横向 k 点的数目,极化值收敛地相对较快,因此我们使用默认值。
您现在已经完成了脚本设置。保存脚本为“BaTiO3_lda.py”。发送脚本到 Job Manager,运行作业。几分钟后计算完成,您就可以检查结果了。
分析结果
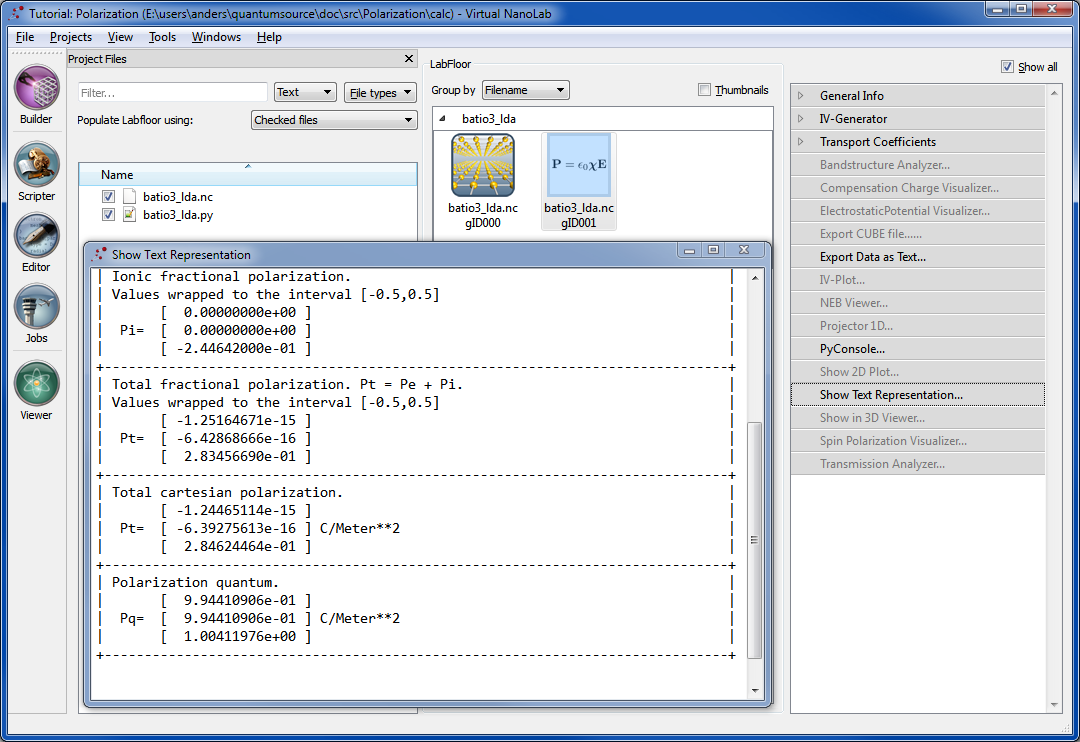
请向下滚动日志文件到末尾,检查报告计算得到的极化,您将找到如下所示的报告。
+------------------------------------------------------------------------------+ | Polarization | +------------------------------------------------------------------------------+ | Electronic fractional polarization. | | Values wrapped to the interval [-0.5,0.5] | | [ -1.25164671e-15 ] | | Pe= [ -6.42868666e-16 ] | | [ -4.71901310e-01 ] | +------------------------------------------------------------------------------+ | Ionic fractional polarization. | | Values wrapped to the interval [-0.5,0.5] | | [ 0.00000000e+00 ] | | Pi= [ 0.00000000e+00 ] | | [ -2.44642000e-01 ] | +------------------------------------------------------------------------------+ | Total fractional polarization. Pt = Pe + Pi. | | Values wrapped to the interval [-0.5,0.5] | | [ -1.25164671e-15 ] | | Pt= [ -6.42868666e-16 ] | | [ 2.83456690e-01 ] | +------------------------------------------------------------------------------+ | Total cartesian polarization. | | [ -1.24465114e-15 ] | | Pt= [ -6.39275613e-16 ] C/Meter**2 | | [ 2.84624464e-01 ] | +------------------------------------------------------------------------------+ | Polarization quantum. | | [ 9.94410906e-01 ] | | Pq= [ 9.94410906e-01 ] C/Meter**2 | | [ 1.00411976e+00 ] | +------------------------------------------------------------------------------+
提示
您也可以选中 LabFloor 上“BaTiO3_lda.py”文件里的极化数据块,点击 Show Text Representation… 以检查结果。
注解
输出应该包含以下 5 个计算值:
- 第一个是电子部分极化 $\mathbf{P}_e$,如在现代极化理论中描述的那样,从占据能带得到贝利相位,继而计算获得电子部分极化。
- 第二个值 $\mathbf{P}_i$ 是完全的离子部分电极 $\mathbf{P}_i = \sum_j Z_j^{ion}\tau_j$,$Z_j^{ion}$ 和 $Z_j^{ion}$ 分别是原子 $j$ 的价电荷和分数坐标。
- 第三个值 $\mathbf{P}_t$ 为总极化,即电子部分和离子部分之和。如在现代极化理论中讨论的,极化是一个多值函数,因此所有的极化是覆盖在 [-0.5,0.5] 区间,也就解释了极化在 z 方向上的正负变换。$\mathbf{P}_e(z) + \mathbf{P}_i(z) = -0.717$ 的总和超出范围,通过加上一部分量化量子(为1),即 $\mathbf{P}_t(z) = -0.717 + 1 = 0.283$。
- 第四个值是笛卡尔坐标系下的总极化 $\mathbf{P}_t$,单位为 C/m2。
- 第五个值是在现代极化理论里介绍过的极化量子 $\mathbf{P}_q$。$\mathbf{P}_t$ 相较于与之相关的 $\mathbf{P}_q$ 偏小。
依据极化现代理论[3],只有两种构型的极化差异才是明确的特性。为了计算四方 BaTiO3 的自发极化,因此也需要计算出以下中心对称无畸变结构的极化:
# Set up lattice lattice = SimpleTetragonal(3.9945*Angstrom, 4.0335*Angstrom) # Define elements elements = [Barium, Titanium, Oxygen, Oxygen, Oxygen] # Define coordinates fractional_coordinates = [[ 0.0 , 0. , 0. ], [ 0.5 , 0.5 , 0.5 ], [ 0.5 , 0.5 , 1.0 ], [ 0.5 , 0. , 0.5 ], [ 0.0 , 0.5 , 0.5 ]] # Set up configuration bulk_configuration = BulkConfiguration( bravais_lattice=lattice, elements=elements, fractional_coordinates=fractional_coordinates )
您可以重复以上步骤计算该结构的极化。结果是所有的极化组分都为 0。四方 BaTiO3 的自发极化符合以上报告的无序结构之值。
计算得到在 z 方向上的总笛卡尔电极值 $\mathbf{P}_t(z)=0.284 $ C/m2 与实验数据 0.26 C/m2 吻合较好[5]。
参考
- [1] X. Lou, Y. Zheng, and B. Wang, J. Appl. Phys., 111, 074102, (2012)
- [2] A. Chanthbouala, A. Crassous, V. Garcia, K. Bouzehouane, S. Fusil , X. Moya , J. Allibe , B. Dlubak, J. Grollier , S. Xavier , C. Deranlot , A. Moshar , R. Proksch , N. D. Mathur , M. Bibes,and A. Barthélémy, Nature Nanotechnology, 7, 101, (2012)
- [3] R. D. (1, 2, 3, 4) King-Smith, and D. Vanderbilt, Phys. Rev. B, 47, 1651, (1993)
- [4] H. D. Megaw, Acta Crystallographica, 15, 972, (1962)
- [5] H. H. Wieder, Phys. Rev. , 99, 1161, (1955)