目录
单轴、双轴应力下的硅
介绍
在本教程您将学习如何使用 QuantumATK 和 Atomistic ToolKit 研究在单轴和双轴应力下硅的电子特性。
特别地,您将学习如何运用结构优化(Optimize Geometry)中的 Target Stress 选项为晶体施加特定应力。然后您将计算并分析应变系统的电子能带结构和有效质量。
本教程的一个重要方面就是施加应力后晶体的对称性。您必须特别注意这一点,为了达到这个目的,您会发现 Brillouin Zone Viewer 插件的实用性。
提示
本教程使用特定版本的QuantumATK创建,因此涉及的截图和脚本参数可能与您实际使用的版本略有区别,请在学习时务必注意。
- 不同版本的QuantumATK的py脚本可能不兼容;
- 较新的版本输出的数据文件默认为hdf5;
- 老版本的数据文件为nc文件,可以被新版本读取。
单轴应力
计算设置
1.在 Builder 里,从数据库导入一个硅的面心立方块体结构,发送到 Script Generator。
2.添加一个 New Calculator:
- 采用默认的 LDA 交换关联势,选择 k 点取样为 9×9×9;
- 设置密度网格截断为 150 Hartree,以更好地描述硅的电子结构。
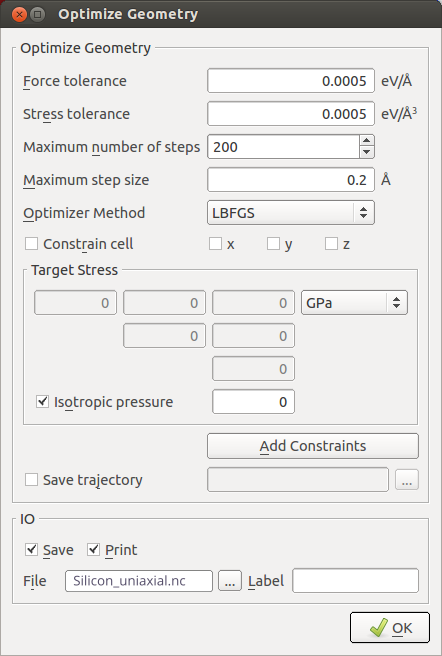
3.添加 OptimizeGeometry,为了执行块体结构的全面优化,设置以下参数:
- 设置 force tolerance 和 stress tolerance 分别为 0.0005 eV/Å 和 0.0005 eV/Å3;
- 不勾选
Constrain cell,保持 Target stress 为 0。
1.添加 Bandsructure 分析:
- 选择每段 201 个点;
- 选择 L,G,X 路径。
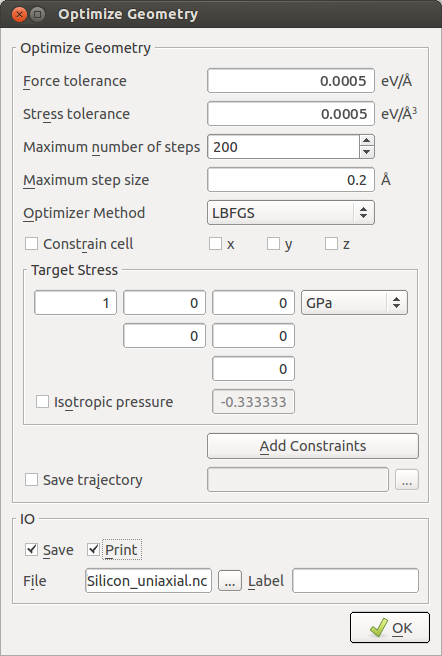
2.添加 OptimizeGeometry,为了施加单轴应力,设置如下参数:
- 设置 force tolerance 和 stress tolerance 分别为 0.0005 eV/Å 和 0.0005 eV/Å3;
- 不勾选
Constrain cell; - 不勾选
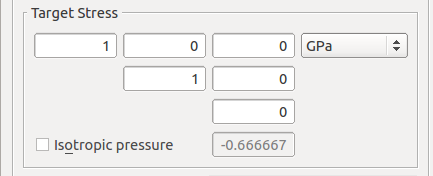
Isotropic Pressure,为应力张量的 $x$ 方向分量设置 1 GPa 的目标应力。
注意
Target Stress(target_stress)的定义为:
如果单一值 $p$ 已给定,它可以理解为内部目标张量处的外部压力,可表述为
$$\sigma = \begin{pmatrix} -p & 0 & 0 \\ 0 & -p & 0 \\ 0 & 0 & -p \end{pmatrix};$$
如果给出目标应力张量,则将其解释为系统的内应力,这意味着对角线上的负数输入值将导致相应方向的压缩,反之亦然。请注意,应力张量是对称的,因此只需要定义上三角形的数值。
请注意实际上这两种情况下符号约定不同!
3.添加 Bandstructure 分析:
- 选择每段 201 个点;
- 选择 L,G,X 路径。
注意
如果给出目标应力张量,则结构的布拉维晶格会自动转换为单胞,以更改晶胞的形状。
如下所述,因在施加应力后晶胞不再是 fcc,布里渊区的高对称点将会改变。但是,在这点的设置上,新晶胞的对称性是未知的,因此您必须在 Python 脚本中手动修改对称点。
4.发送脚本到 Editor,定位至最后的 Bandstructure 分析模块。将路径中的 B 替换为 X;关于修改布里渊区的详解下一章节中可见。
1 # ------------------------------------------------------------- 2 # Bandstructure 3 # ------------------------------------------------------------- 4 bandstructure = Bandstructure( 5 configuration=bulk_configuration, 6 route=['L', 'G', 'B'], 7 points_per_segment=201, 8 bands_above_fermi_level=All 9 ) 10 nlsave('Silicon_uniaxial.nc', bandstructure)
您可以在此处下载完整的脚本:↓Silicon_uniaxial.py。
5.保存并发送脚本到 Job Manager 运行计算,只需等待不足一分钟的时间。
对称性的考虑
在分析应变硅的电子结构前,您需要理解 QuantumATK 和 ATK 如何处理布里渊区和高对称点符号。
将优化结构(gID000)和应变结构(gID002)从 LabFloor 拖拽到 Builder。
利用 Bulk Tools ![]() Brillouin Zone Viewer… 画出每个结构的布里渊区。
Brillouin Zone Viewer… 画出每个结构的布里渊区。
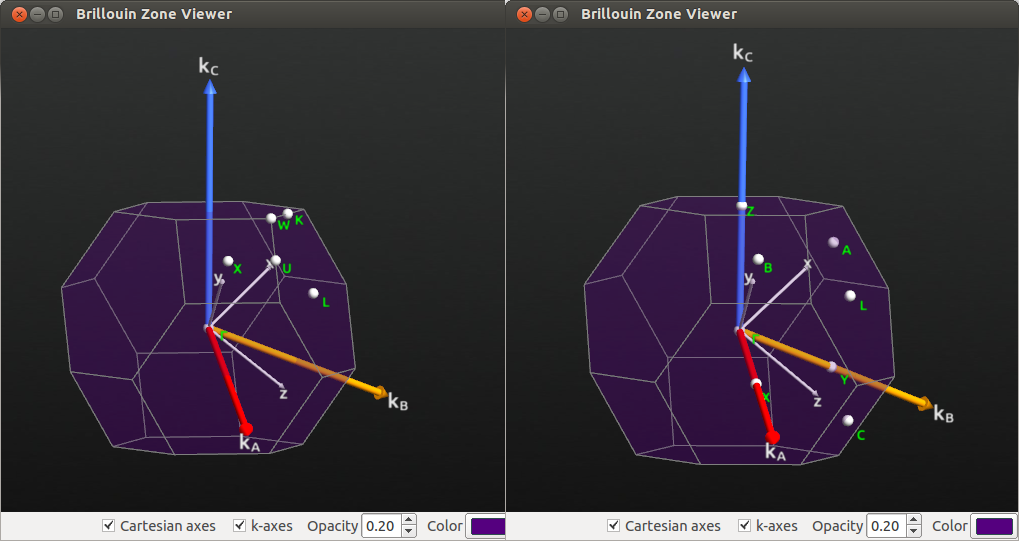
图 82 当使用FaceCenteredCubic 布拉维晶格时,fcc 块体硅的布里渊区(左图)。当布拉维晶格变为 UnitCell 类型时,高对称点的符号会根据图(右图)改变。
应变面心立方晶胞的 UnitCell 描述的高对称点和面心立方对称点相关,如下所示:
- A,B,C都对应于未应变 fcc 布里渊区域中的 X 点。
- 通过增加应力,您可以看到 B 和 C 仍然是退化的,但 A 没有随 B和 C 退化。这在四方对称性中是合乎逻辑的。
- L 点仍被称为 L,且在UnitCell 符号中随 X,Y,Z 退化。
正如预期,在施加单轴应力后,晶体实际上是四方的(空间群141),可以通过激活 stash 区的应变晶胞并点击 Bulk Tools ![]() Crystal Symmetry Information,然后单击 Detect 得到验证。
检查晶格参数时,您会看到,仍如预期那样,由于单轴变形,3 个晶格矢量都在 X 轴上伸长,并在 Y 和 Z 上(弹性响应,泊松效应)收缩。
Crystal Symmetry Information,然后单击 Detect 得到验证。
检查晶格参数时,您会看到,仍如预期那样,由于单轴变形,3 个晶格矢量都在 X 轴上伸长,并在 Y 和 Z 上(弹性响应,泊松效应)收缩。
分析结果
电子能带结构
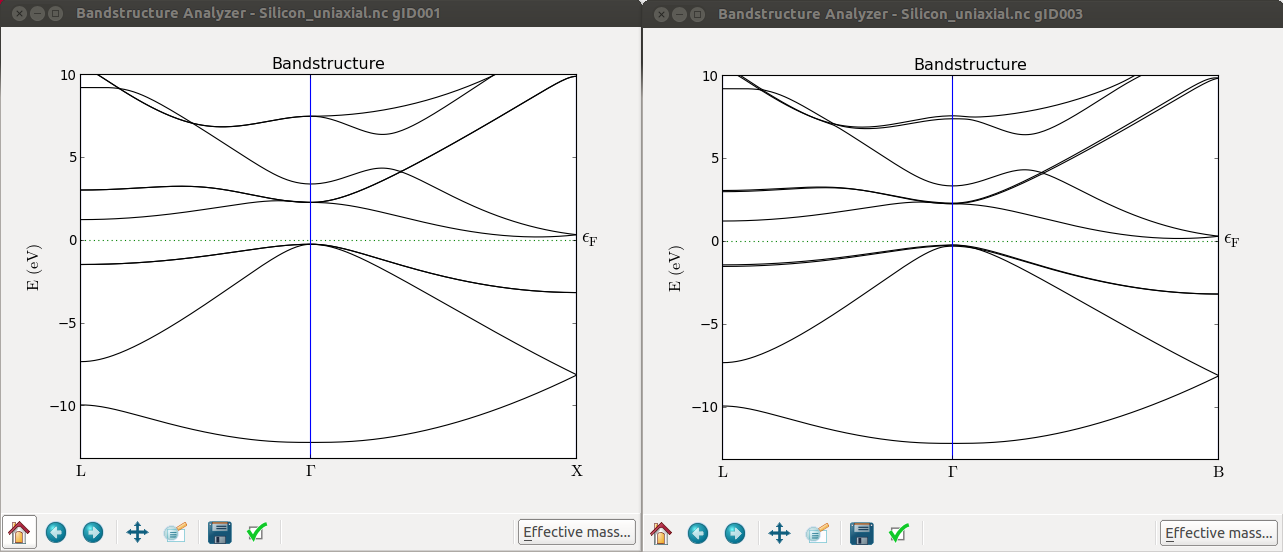
现在画出优化晶胞和受单轴应力晶胞的能带结构图。从 LabFloor 中选择计算 Bandstructure 项目,然后用 Bandstructure Analyzer 插件绘图。
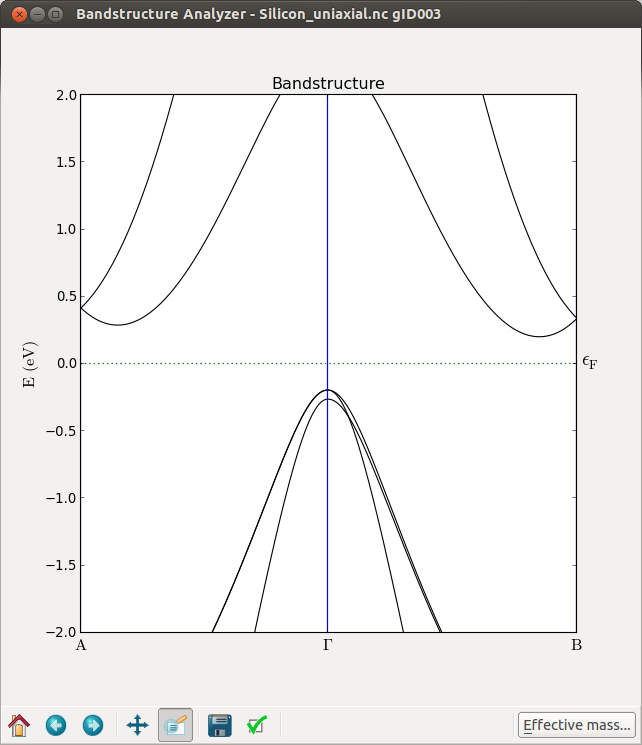
从以上这些图中,您可以立即看出在伽马点,价带顶部分裂开。然而更有趣的是可以观察到 $\Delta$valley 不再退化。为更清楚地看到这种效应,您可以计算沿 A-G-B 路径的能带结构。
通过进一步地检查能带结构,您可以得出以下单轴应变硅的相关结论:
- L 仍然退化
- 6 倍的 $\Delta$valley 分裂成 2+4
然而,在该模拟中带隙的绝对值是不正确的,因为采用了 LDA 交换关联函数简化。
有效质量
考虑应变对有效质量的影响也是非常有趣的。
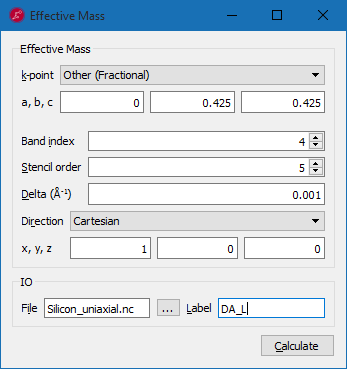
从应变结构的能带结构图中,单击 Effective Mass 按钮。
参照图中举例子计算指数为 4 的能带沿不同方向 $\Delta$valley 的有效质量。
- $\Delta_A$ 的纵向质量:分数坐标 [0, 0.425, 0.425],沿笛卡尔方向 [1, 0, 0];
- $\Delta_A$ 的横向质量(1):分数坐标 [0, 0.425, 0.425],沿笛卡尔方向 [0, 1, 0];
- $\Delta_A$ 的横向质量(2):分数坐标 [0, 0.425, 0.425],沿笛卡尔方向 [0, 0, 1];
- $\Delta_B$ 的纵向质量:分数坐标 [0.425, 0, 0.425],沿笛卡尔方向 [0, 1, 0];
- $\Delta_B$ 的横向质量(1):分数坐标 [0.425, 0, 0.425],沿笛卡尔方向 [1, 0, 0];
- $\Delta_A$ 的横向质量(2):分数坐标 [0.425, 0, 0.425],沿笛卡尔方向 [0, 0, 1];
你将得到以下结果:
- $\Delta_A$ (2 倍退化)的纵向质量:0.91
- $\Delta_A$ 的横向重量:0.185(无分裂)
- $\Delta_B$ (4 倍退化)的纵向质量:0.898
- $\Delta_B$ 的横向质量:0.188 和 0.186
因此,虽然所有的纵向和横向质量都非常接近原始的 $\Delta$valley 质量(0.903 和 0.186,可计算未应变晶体得到),您会观察到因对称性破坏导致的分裂。
为获得更多硅有效质量计算的详解可参考教程 Effective mass of electrons in silicon。
作为练习,我们鼓励您在 L 点研究质量,并探讨可能的对称性断裂。
双轴应力
将优化(未应变)的硅结构发送到 Scripter,像上一章节一样设置 New Calculator,OptimizeGeometry 和 Bandstructure。
施加一个双轴应力,在 Optimize Geometry 对话框里 Target Stress 区域的应力张量中设置 xx 和 yy 组分均为 1 GPa。
运行计算前,将脚本发送到 Editor,修改布里渊区路径为如上所述的 L,G,B,执行计算。
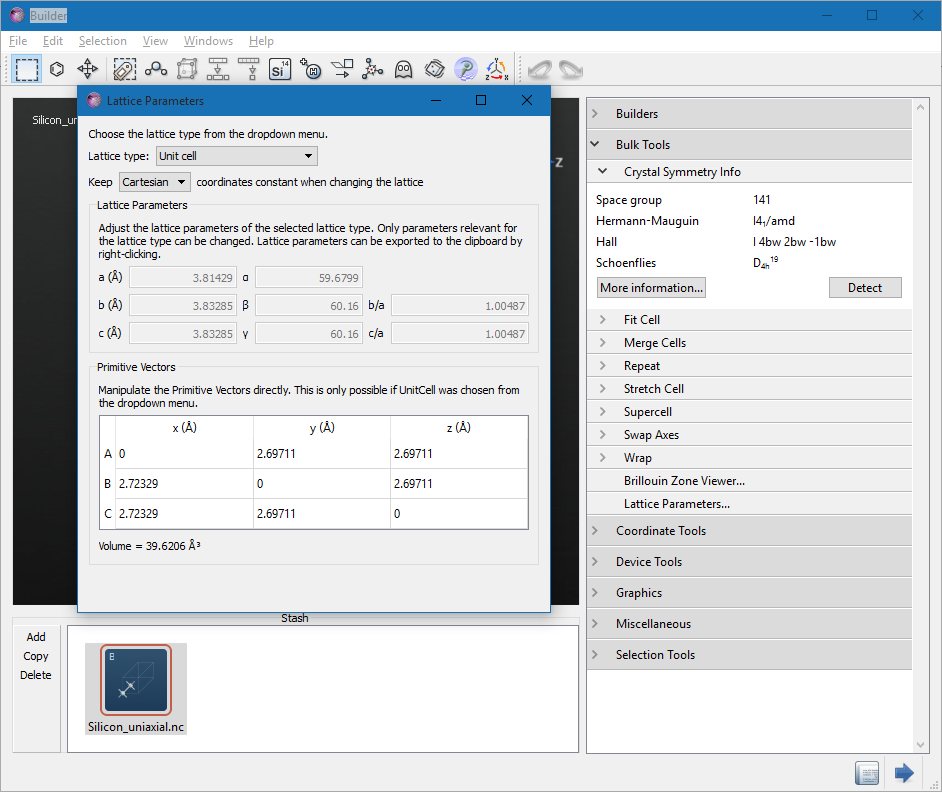
在这种情况下,立方晶格也变形为四方对称。为了可以清楚地观察,将优化后的应力结构拖放到 Builder 并应用超胞转换,如下图所示。
点击 Bulk Tools ![]() Lattice Parameters,您可以看到畸变晶格参数为 5.44 Å 和 5.38 Å。因此,有效地双轴应力相当于沿 [001] 方向的单轴应力,但具有相反的符号。
Lattice Parameters,您可以看到畸变晶格参数为 5.44 Å 和 5.38 Å。因此,有效地双轴应力相当于沿 [001] 方向的单轴应力,但具有相反的符号。