伏安特性曲线（IV 曲线），即电流-电压曲线。这里的电压指的是源漏偏压，电流指的是漏电极电流。IV 曲线是双电极器件体系性能模拟的主要目的。

IV 曲线通过计算不同偏压下的电流得到。特定偏压 $V_b$ 下的电流 $I$ 可以由下求得：

$$ I = \frac{e}{h}\int _{-\infty}^{+\infty} T(E;V_b) [f_L(E;E^L_F-V_b/2)-f_R(E;E^R_F+V_b/2)] dE $$

其中 $f_L(E;E^L_F-V_b/2)$、$E^L_F$ 和 $f_R(E;E^R_F-V_b/2)$、$E^R_F$ 分别为左右电极平衡态时的费米能级和费米分布。

积分限的确定。由于费米分布在 $-\infty$、$+\infty$ 很快趋近于 0 和 1，而在费米能级处呈台阶状，因此实际积分的范围可以确定为（$E^L_F-V_b/2 - nk_B T$,$E^R_F + V_b/2 + nk_BT$），之所以增加 $nk_B T$ 是为了考虑费米分布的宽度。

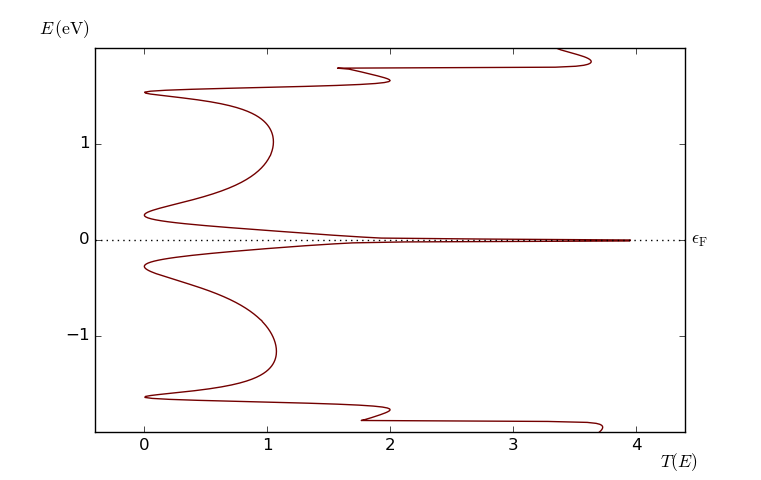
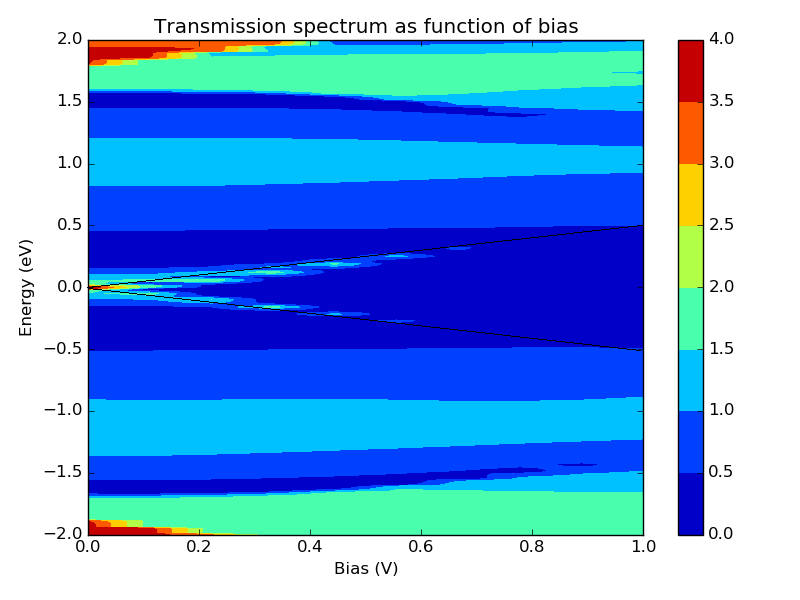
$T(E;V_b)$ 为电子透射概率函数谱，表示不通能量的电子透射的概率。注意到，一般情况下， $T(E)$ 的形状依赖于偏压 $V_b$（见下图），因此通过自洽的非平衡态格林函数方法可以更好的计算电流。如果忽略 $T(E)$ 对偏压 $V_b$ 的依赖，则可以通过零偏压下的平衡态透射谱计算线性响应电流。

QuantumATK默认采用自洽的非平衡态格林函数（NEGF）方法计算非零偏压下的电流，此时体系的电子态处于非平衡态。

由于这时考虑了透射谱形状随偏压的变化（见上一节图），因此如下所示的体系出现了负微分电阻（NDR）效应。

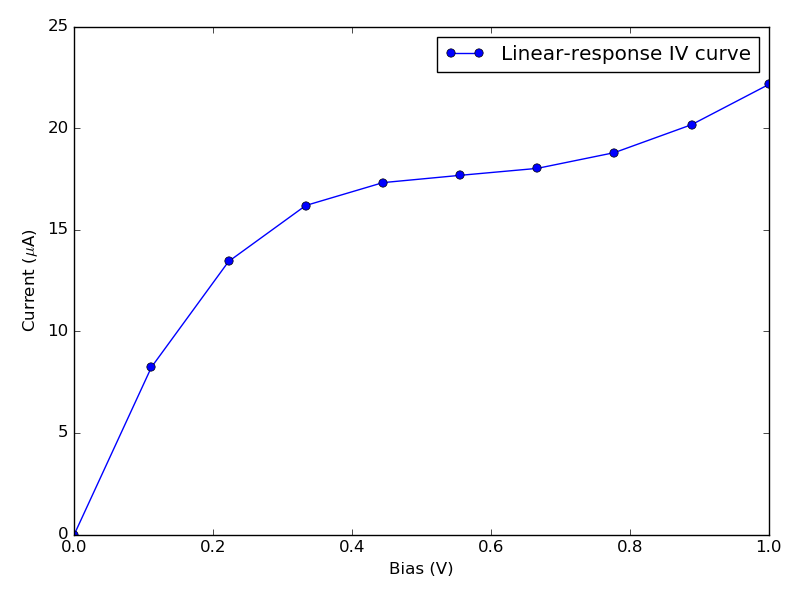
另一种计算电流的方法是仅计算零偏压下的电子透射谱曲线，而后在同一条曲线上通过改变积分偏压窗口求得不同的偏压下的电流。由于电子透射谱在全能量范围里始终为正，因此无法出现预期的 NDR 效应。上述体系的线性响应电流如下图。

QuantumATK提供计算IV曲线的IVCurve计算类型，可以直接对偏压点进行循环采样，并给出IV曲线。使用IVCurve进行计算的好处是：

• 直接一步获得全IV曲线；
• IVCurve支持在偏压上进行多级并行，可以使用几百核同时对多个偏压点进行并行计算。(更多并行计算的设置细节请参考：QuantumATK并行计算）
• 直接使用IVplot进行分析。

• 将完成优化的结构传送至Scripter，添加NewCalculator、Analysis-IVCurve；
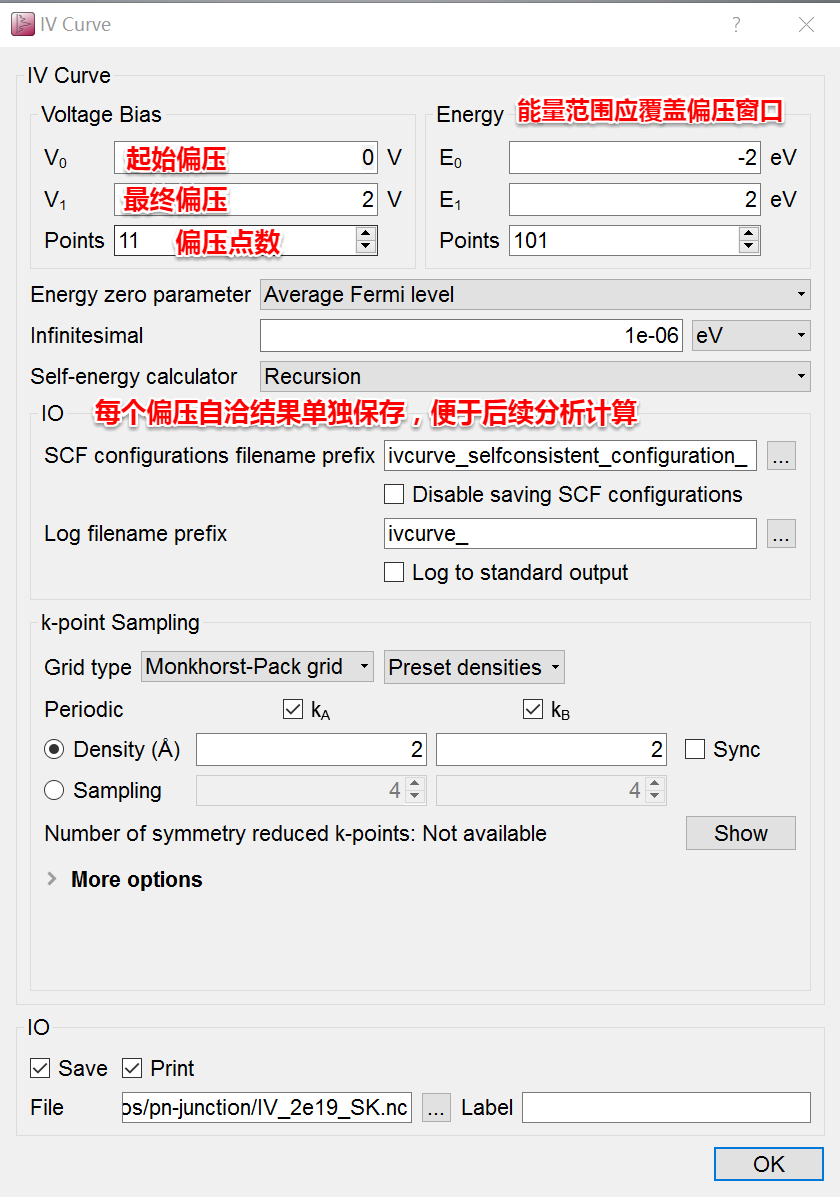
• 在New calculator 和 IVCurve 中正确的选择计算方法和参数。需要注意此时电流计算仍然是进行一系列TransmissionSpectrum的计算，因此除电压扫描设置之外（下图），其他与 TransmissionSpectrum 完全相同（参见：使用QuantumATK研究电子输运）；

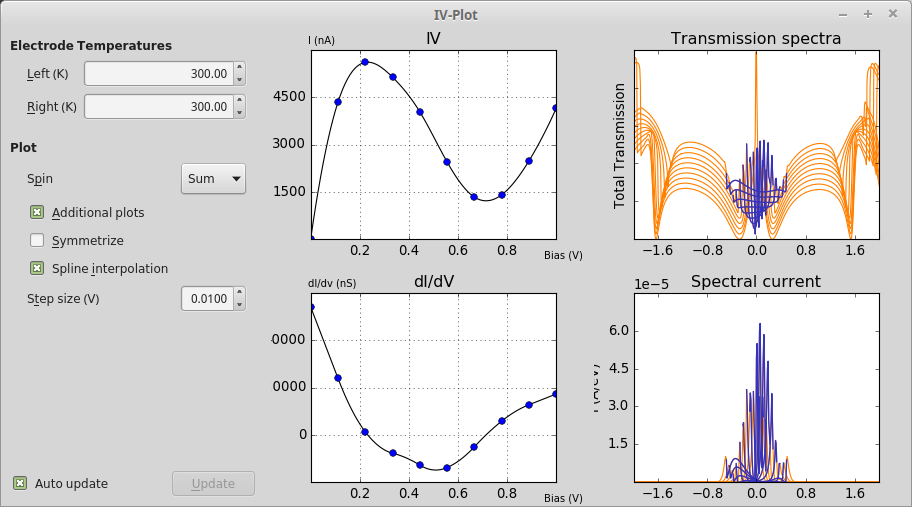
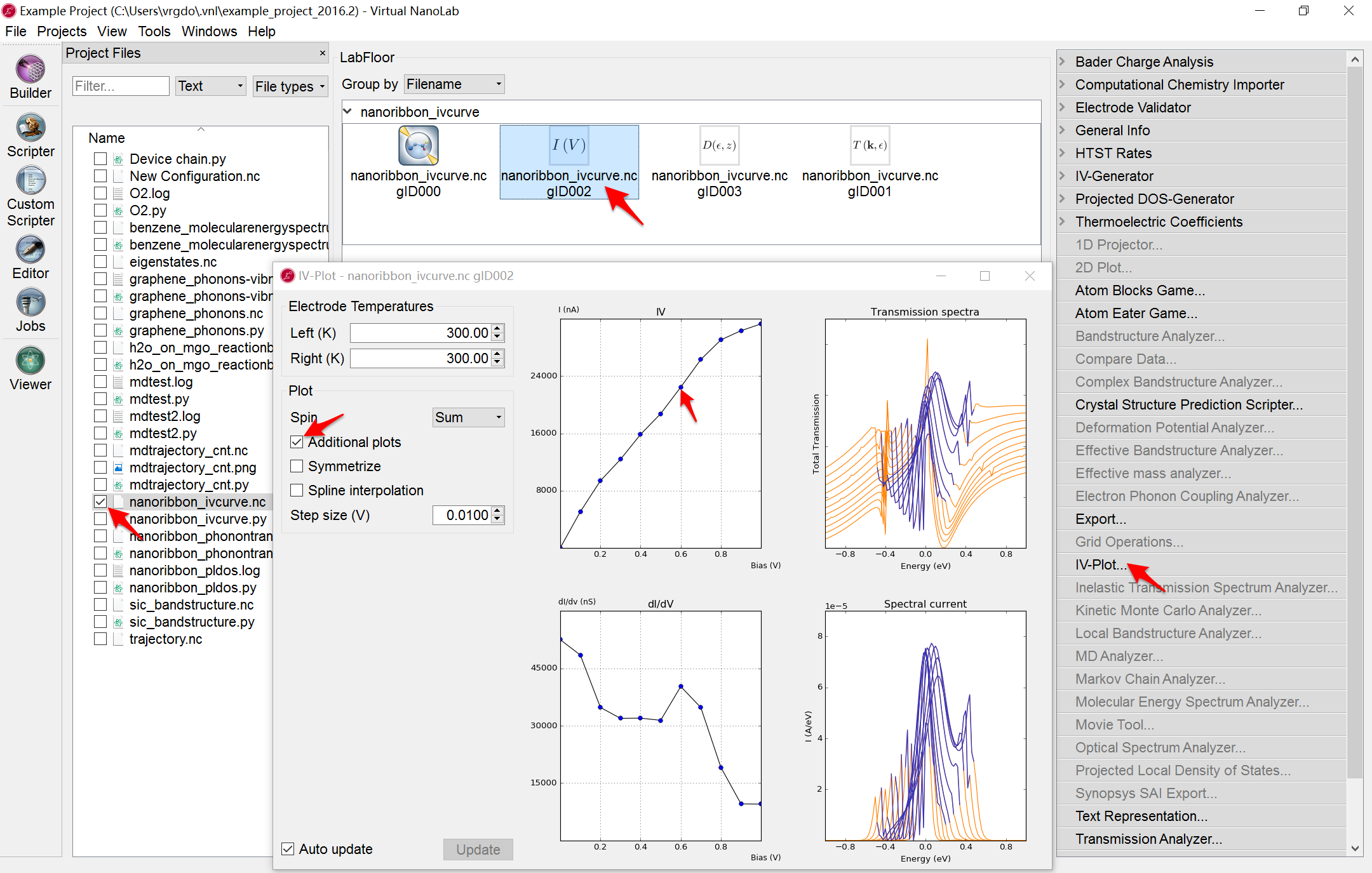
• 使用IVplot工具可以直接分析IV曲线，IV plot工具提供IV曲线、微分电导曲线（dI/dV）、所有偏压下的透射谱和谱电流曲线、自旋分析等多种工具（下图）。

使用者还可以按偏压点逐点手动完成透射的自洽计算，并使用VNL图形工具上的IV generator生成IV曲线。这种方法的好处是：

• 可以更灵活的对偏压进行取点，比如可以先进行粗略大范围取点，了解体系在不通偏压下的收敛情况和电流大小，再逐渐补充精细的偏压点。
• 使用者对每个偏压下的收敛状况单独控制。

• 完成计算体系的结构优化后，添加New Calculator、Analysis-Transmission设置新计算；
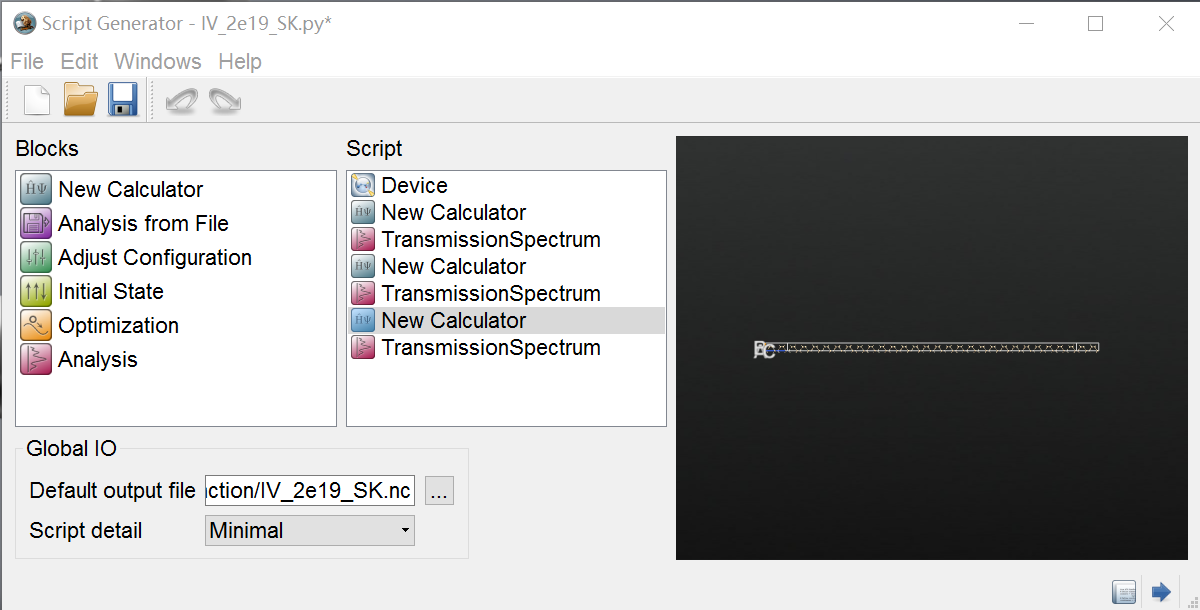
• 可以设置一系列的“New Calculator、Analysis-TransmissionSpectrum”用于不同偏压（下图）

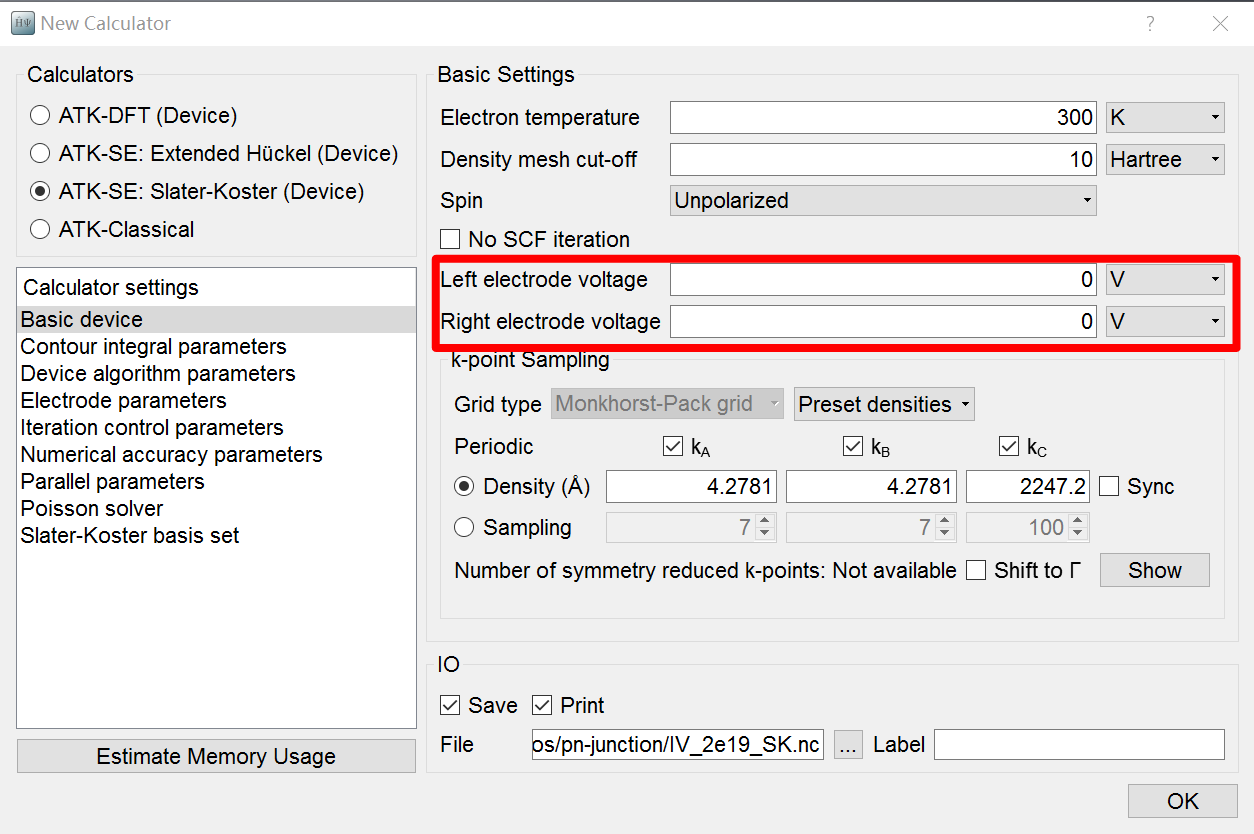
• 在每个New Calculator里正确设置需要的左右电极电压
• 提交完成全部计算

• 勾选输出的nc文件，在LabFloor里选中所有的TransmissionSpectrum，使用右侧的IVGenerator工具生成IVCurve曲线

• 线性响应电流：http://docs.quantumwise.com/tutorials/linear_response_current/linear_response_current.html
• Python类关键词参考：IVCurve