分子动力学基础

所谓分子动力学（MD）模拟，是在预先确定条件下（比如温度，压力，应力，外力等等）模拟原子和分子运动的一种方法。分子动力学模拟可以用来研究纳米尺度下的动力学过程，还可以用来计算相图、扩散系数和各种响应函数等诸多性质。

QuantumATK（和 NanoLab）可以使分子动力学模拟变得非常简单：只需要向构型（configuration）添加所需的计算器（calculator）和分子动力学模块（MolecularDynamics block），就可以开始计算了。对于不同类型的模拟，什么样的参数和设置是最合适的，在这里给出了一些指导方针。本文简要介绍 QuantumATK 中分子动力学（MD）功能，并且一步步的解释了如何正确地设置模拟过程以得到想要的结果。

分子动力学模拟本质上是对给定初始构型中原子运动的牛顿方程求数值解。这通常是通过对有限时间步长进行积分计算得到的。原子之间的相互作用（也就是原子间力）可以通过不同的方法（可以是密度泛函理论（DFT）或经典力场）来进行计算。这些力决定了原子的加速度并且使得原子的位置和速度传递到下一个时间步长。多次重复这个过程会产生一系列的构型快照，这些快照描述了系统在相空间中的运动轨迹，从而可以进一步从中分析提取出想要的性质。

在设置模拟之前你需要选择你所感兴趣的计算类型。要考虑得因素有：总能量是否守恒（孤立体系中的情况）？模拟体系与热浴（heat bath）之间的耦合时是否要保持温度不变？系统是否受到外加压力或者应力？基于这些考虑我们应该选择一套合适的模拟参数：时间步长大小， 积分步长的数量（模拟持续的时间），积分算法，初始温度，约束条件等等。

类似于真实的实验，进行分子动力学模拟需要一些实证上的知识和经验。在本例中，你将会了解分子动力学模拟的基本组成部分，以及如何使用 QuantumATK 的分子动力学模块来进行分子动力学模拟。

将这些技巧应用于一个简单、著名的测试体系——块体硅，你将逐步学习到如何选择时间步长大小，如何控制温度和压力，以及如何通过约束条件来固定某些原子。

正如介绍中所述，分子动力学模拟基于的是求解牛顿运动方程。微正则系综（NVE）是分子动力学模拟中最原始和纯粹的形式，其中原子数（N），体积（V）和总能（E）守恒。这些条件对应了一个完全孤立体系，而产生的系综也被称为微正则系综。

在这个章节，你将了解如何运行微正则系综（NVE）模拟，以及如何通过监测总能（此处应为定值）来评定系统的特性。你将会学习到如何为给定系统选择合适的时间步长大小。

打开 VNL，创建一个新的项目并命名，打开此项目。点击工具栏的按钮启动 Builder。 在 Builder 中，点击Add ‣ From Database。搜索 Silicon 并添加到 stash 栏中。

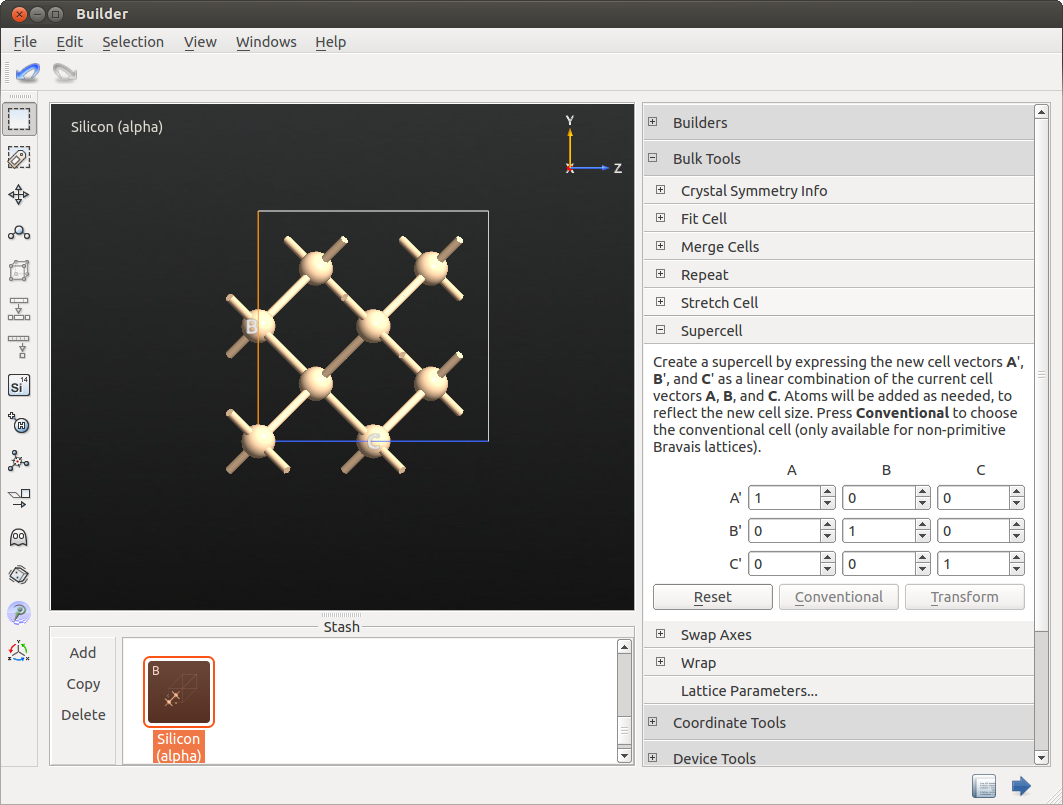
初始的硅的单胞的晶格矢量是非正交的。尽管在这种晶胞上可以进行分子动力学模拟，但是使用正交晶胞往往更方便一些（尤其是在晶胞尺寸在模拟过程中发生变化的情况下）。你可以使用 Builder 面板中 Bulk Tools ‣ Supercell。点击 Conventional 和 Transform 使初始单胞变为常规的立方晶胞。

此外，通常有必要增大硅结构的尺寸以包含更多的原子，因为这样可以改善所要计算的可观测量的平均值，并且减少小的模拟晶胞与其周期重复构象相互作用所导致的有限尺寸效应（晶胞矢量的长度最好大于两倍的势的相互作用距离）。通过点击 Bulk Tools ‣ Repeat 选择 4 x 4 x 4 的重复来增加结构的尺寸。这将得到总共 512 个原子。 

接着使用 Builder 窗口右下角的 图标将结构送到 Script Generator。

接下来，你将设置运行分子动力学计算中将要用到的计算脚本。对于 Si-Si 相互作用，我们将使用 Tersoff 型的势。实际的分子动力学模拟也将在这里设置。

在 Script Generator 中

• 添加一个 New Calculator。
• 添加 Optimize > MolecularDynamics 模块。

双击 New Calculator 选择 ATK-Classical 计算器和 Tersoff_Si_1988 势¹⁾。由于我们不需要保存或者打印初始构型的附加信息，所以不选 Save和 Print。

现在，双击 MolecularDynamics 模块。首先，看一下 Type 下拉列表。这一设置非常重要，它可以让你选择使系统处于什么样的积分算法和物理系综下模拟。对于第一个模拟，我们设置为 NVE Velocity Verlet 类型。这个设置选择了恒定粒子数（N），恒定体积（V）和恒定总能（E）的系综，并且使用了 velocity verlet 积分算法²⁾。

设置 Steps 的数量为 1000，Log Interval 为 5。后者的值决定了当前构型的快照多久被写入硬盘一次。过小得log interval 值会降低模拟的速度，而且会在较大体系计算中产生很大的输出文件。

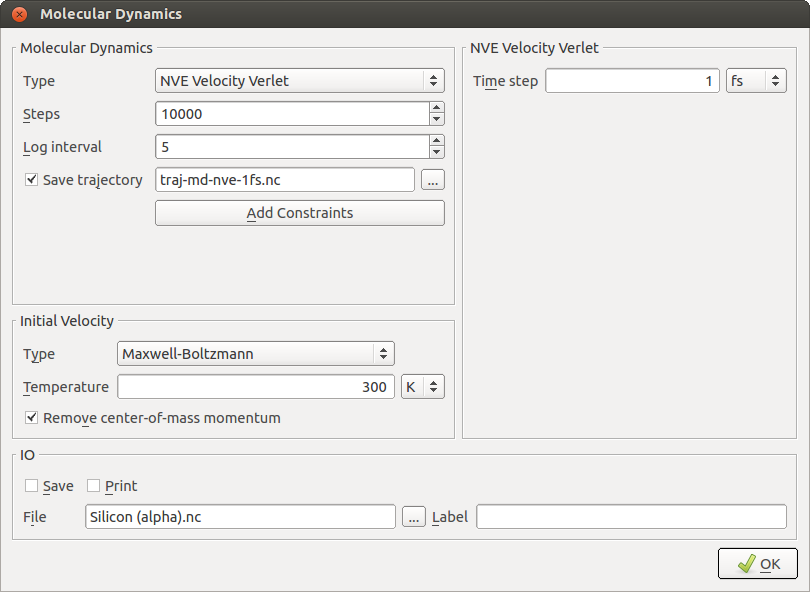
键入一个合适的轨迹文件名，比如 traj-md-nve-1fs.nc。设置 Initial Velocity 为 Maxwell-Boltzmann，选择 Temperature 为 600 K。这将给每个原子一个随机的初始速度，对应于 600K 的麦克斯韦-玻尔兹曼分布。另外，选择相应的复选框，质心的动量将会在分布中被去除从而防止模拟过程中整个系统的漂移。

Time step 在分子动力学模拟中是一个关键参数，它决定了数值积分方案的精准度和效率。后续我们会研究它的作用，但是在最开始，我们保持他的默认值 1 fs。

之后，由于轨迹（trajectory）已经被保存，你可以点掉 Save 和 Print 这两个选项。 最终，你的分子动力学设置应该如下图所示。

点击 OK 并保存脚本为 md-nve-1fs.py。然后发送脚本到 Job Manager (再次使用按钮)并开始模拟。几分钟后即可完成模拟。

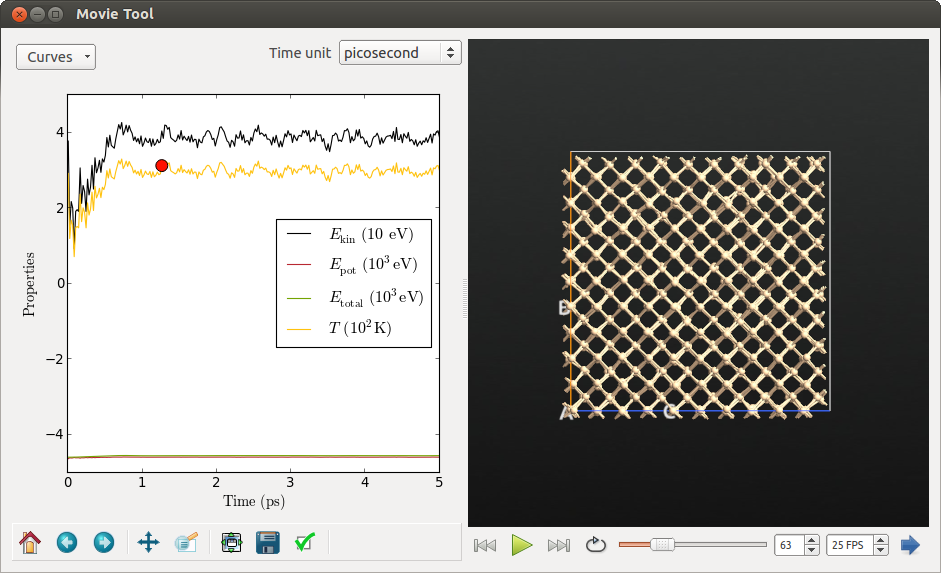
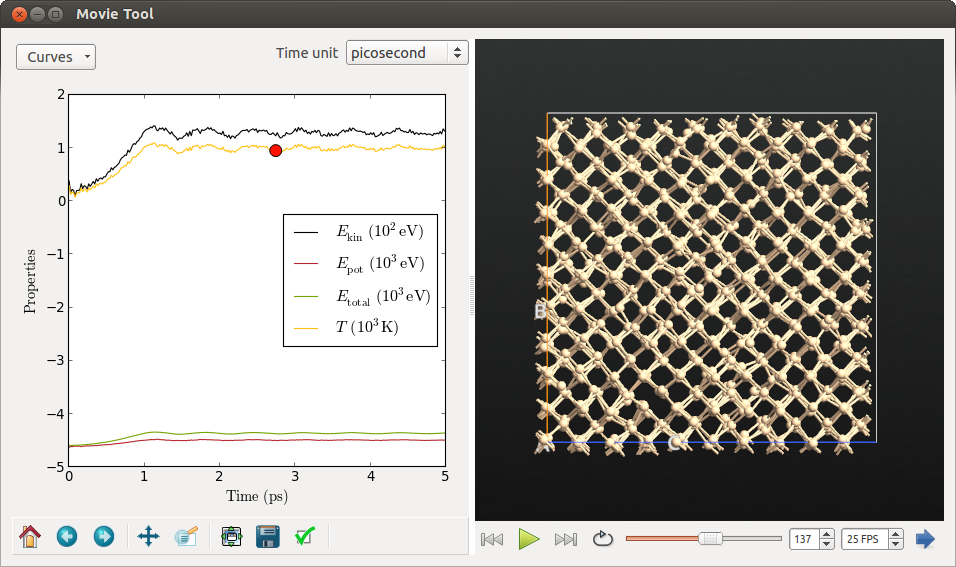
使用Movie Tool插件，你可以研究系统的温度、动能、势能以及总能随模拟时间变化的函数。同时，原子运动的动画也将同时展示。选择LabFloor中的 traj-md-nve-1fs.nc 然后点击 Movie Tool 插件。

如果你查看一下温度曲线，你就会发现温度如何迅速下降然后在 300 K 左右进行振荡。这是因为显示的温度是系统的即时温度，是通过原子的动能以及公式 $E_{kin}(t)=3/2Nk_BT(t)$ 计算得出的。由于原子不是孤立的，而是与晶格里的其他邻近原子相互作用，他们的初始动能将会部分地转化成势能。由于初始构型很接近势能最小值，接近一半的动能被转化，导致温度下降大约50%。实际上，如果你仔细观察势能曲线，你会看到相反的情形（势能迅速升高，然后在一个固定值左右进行振荡）。

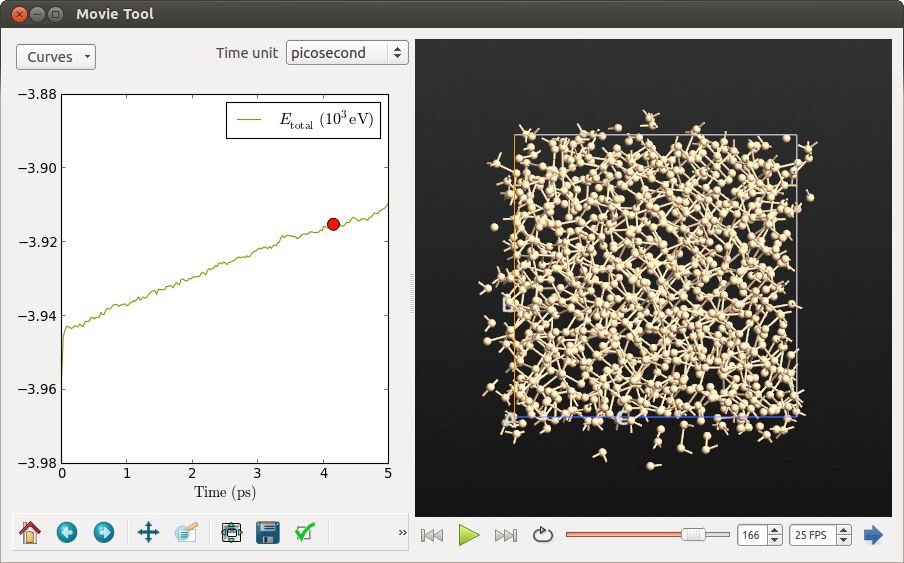
由于你模拟了一个微正则（NVE）系综，一个重要的监测量是总能的守恒。使用能量曲线图下面工具栏里的缩放工具，放大总能曲线。你会看到一个类似于（但可能不会完全一样）下图的曲线。

总体上，系统的能量保持在一个相对于平均值小于 $10^{-5}$ 量级上的小涨落内。重要的是，平均值是固定的，没有发现漂移。这些发现表明所选分子动力学（MD）的设置较为恰当。

我们看看如果选择了一个很大的时间步长大小会发生什么。修改初始温度为 5000 K 和时间步长大小为 5 fs，重复上述模拟。你可以再一次使用MolecularDynamics 模块，也可以将 md-nve-1fs.py 直接拖拽到 Editor 按钮。记得改一下轨迹（trajectory）文件名。保存这个新修改的脚本为 md-nve-5000K-5fs.py 并运行。

如果你在 Movie Tool 中可视化轨迹模拟的结果，你将发现原子的运动增强。结构甚至会部分融化。如果你再次放大总能曲线，你会观察到其值显著的漂移。由于在此温度下时间步长被选的太大，能量不再变得那么恒定。

核心要点是，大的时间步长看上去会提高模拟效率，但实际上会增加运动方程数值积分方案的误差。原子力在一个积分步长内近似守恒的基本假设失效。本质上，所选时间步长应该足够小以解析原子的最高振动频率（也就是说，其应该远小于最小的振动周期）。所以如果你有轻原子（比如氢），那么通常你需要选择比只有重原子(比如金)时更小的时间步长。如果在你的计算中有不同的元素，且温度较高或者原子远离其平衡构型（即粒子受到很大的力）时，也需要选择小的时间步长。如果你不知道使用多大的时间步长，对于多数系统你可以选择 1 fs 作为一个比较安全的开始。通过监测感兴趣的条件下的 NVE 模拟总能是否守恒，你可以对大一些的时间步长值进行评估。

另一个需要知道的分子动力学模拟的重要方面是，一个系统需要一定的时间来与所设置的外界温度和压力达到平衡。在本例中，系统温度和总能总的涨落的量级达到稳态用了大约 400 fs。这点很重要，因为任何可观察量的测量需要在系统达到平衡之后才可以实现（除非你要研究非平衡现象）。在本例中你需要等待至少 400 fs。总的来说，分子动力学模拟的平衡时间最大可以直到几百纳秒（比如在生物分子或者聚合物系统），并且依赖于系统中出现的最长的弛豫时间。所以你应该仔细检查，所感兴趣的可观察量是否在你的模拟中达到稳态。

在接下来的部分你将学到如何在 NVT 系综下进行分子动力学模拟，也就是温度可控的模拟。NVT 系综也叫作正则系综，它与微正则系综 NVE 主要的差别为：系统不再是孤立的，而是可以和一个周围虚拟的热浴进行能量交换。

你将使用和上面部分同样的系统——块体硅，使用 ATK-Classical 计算器（calculator）以及 Tersoff-potential。

你将以室温下结构的平衡态为开始。用上述同样的方法和同样的模块（NewCalculator 和 Optimize ‣ MolecularDynamics) 来准备脚本。实际上，如果你先前的脚本还存储在 ScriptGenerator 里，你可以重新使用它。

双击 MolecularDynamics 模块打开设置。由于我们要运行 NVT 系综下的模拟，我们这回需要选择一个不同的 Type。对于 NVT 模拟，QuantumATK 提供了四种选项：

1. NVT Berendsen³⁾ 
2. NVT Nose Hoover⁴⁾
3. Langevin⁵⁾
4. NVT Nose Hoover Chain⁶⁾

在 MolecularDynamics 界面工具栏，选择 NVT Nose Hoover chain 类型。设置步数为 5000 和 log interval 为 20。保存轨迹（trajectory）到文件 traj-nvt-nosehooverchain-300K.nc 选择 Maxwell-Boltzmann 初始速度为 300 K。时间步长默认 1 fs，Reservoir temperature （虚拟热浴温度）选择为 300 K，Thermostat timescale 选择 100 fs。后面的值决定了系统温度多快达到虚拟热浴温度。我们将会在本部分后面仔细研究这个参数的影响。Final temperature值总是和虚拟热浴温度同步，除非你在这里明确的指定一个不同的值。这个参数可被用来在模拟过程中线性增大或线性减小温度（参见参考手册 NVTNoseHooverChain）。Thermostat chain length 这个参数决定了调用多少个并发的调温器（thermostat）来控制温度。默认值三可以在多数情况下够用。只有当你面临一个强的持久的温度振荡时，可以增加该值以获得更稳定的模拟。

点击 OK 关闭分子动力学设置，发送脚本到 JobManager 并运行。

模拟结束，轨迹文件将会出现在 Lab floor。使用 Movie Tool 打开。

观察一下温度曲线。你会发现在一个短暂的初始平衡时期之后，曲线在所选的模拟热浴温度 300 K 附近轻微涨落。实际上，这与之前部分 NVE 模拟的结果看上去没有太大的不同。与 NVE 模拟不同的是，系统最终平衡温度不依赖于通过 Maxwell-Boltzmann 分布设定的初始温度。现在让我们更细致的观察。

打开上一个模拟的 Script Generator。双击 MolecularDynamics 模块改变虚拟热浴（Reservoir）温度为 1000 K。Maxwell-Boltzmann 温度为默认 300 K。最后，将文件名改为 traj-nvt-nosehooverchain-1000K.nc。关闭设置，运行脚本。

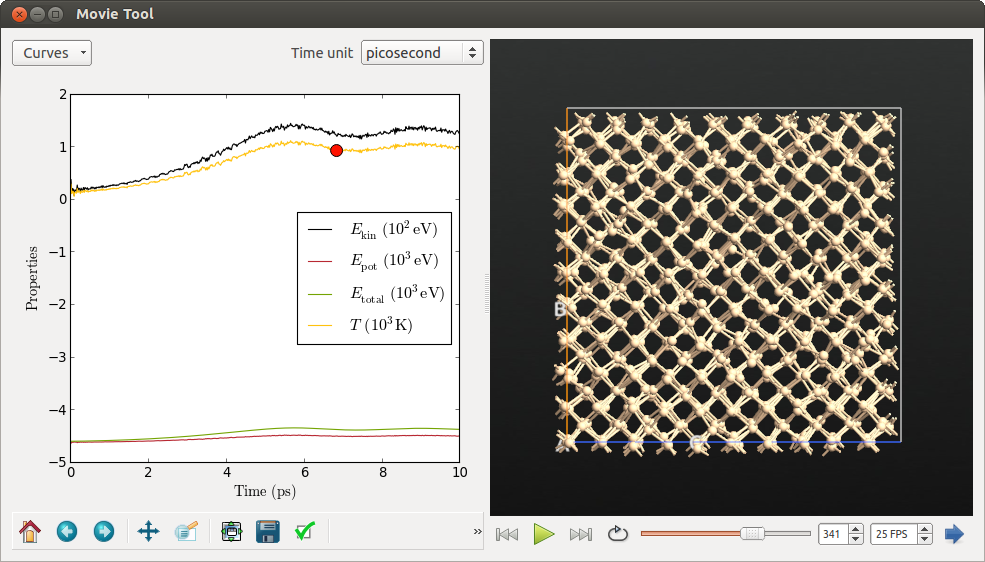
结果应该与下图类似。

温度曲线起始于初始值 300 K（通过 Maxwell-Boltzmann 分布选取）。接着，由于系统与热浴接触，温度迅速提升到虚拟热浴（reservoir）温度 1000 K。

你也会注意到总能的增加。与 NVE 模拟相比，这并不表示参数选取不合适，而是反映了系统在与虚拟热浴交换能量这一的事实。

与上一个模拟相比，在模拟过程中原子的动作增大。如果你将虚拟热浴温度提升到更高的值（比如 3000 K），你将会发现晶体开始融化和部分非晶化。对晶体高温退火实际上是一个产生非晶结构材料的通常方法。你将会在 创建无定形材料结构模型 这个例子中学到更多关于这个方法。

上面说过，调温器（thermostat）时间标度参数可以控制向目标温度接近过程的粒子速度。现在你将使用一个不同的调温器时间标度值来重复同样的模拟。打开上一个模拟的脚本，打开 MolecularDynamics 设置。保持其他设置不变，改变 Thermostat timescale 值为 500 fs。为了完全获取这个持续很久的平衡相，增加步数到10000，改变文件名为 traj-nvt-nosehooverchain-1000K-500fs.nc。关闭设置，开始模拟。

模拟结果应该与下图类似。

定性地，结果与上一个模拟非常类似。然而，你会注意到温度达到虚拟热浴温度过程现在变得很慢。

总体上讲，一个小的调温器（thermostat）时间标度参数使得与虚拟热浴的耦合更加紧密，从而使系统温度更加紧密的保持在虚拟热浴温度。然而，如此紧密的调温器耦合通常伴随着对粒子自然的动力学显著的干扰。所以，当你需要对扩散或者振动等动力学性质进行准确的测量时，你需要使用比较大的热耦合系数或者考虑在 NVE 系综上进行模拟以避免调温器（thermostat）对系统不符合自然规律的作用。

除了 Nose-Hoover chain 温度器（thermostat）之外，你还可以选择其他算法，比如 NVT Berendsen, Langevin, 或者NVT Nose-Hoover。最后的这个方法是 Nose-Hoover-Chain 方法更早和更简单的版本，它的呈现更多的是出于历史原因。如果可能，你应该优先选取 Nose-Hoover-Chain 方法，因为它给出许多更好的结果。 Berendsen 调温器（thermostat）提供一种算法有效的抑制温度振荡，使得在一些情况下系统更稳定。但是，相比于 Nose-Hoover-Chain，它不能精确得到正则系综，尽管偏差非常小。由于这个原因，Berendsen 方法主要用在平衡态模拟，主要是在需要强健温度控制的情况中。 你可以为 NVT 模拟选择的第三个调温器（thermostat）类型是 Langevin 算法。这个算法求解 Langevin 方程，明确地在牛顿运动方程中包含摩擦以及随机碰撞力以模拟粒子与虚拟热浴之间的相互作用。 不同于其他温度器（thermostat）类型，Langevin 恒温器（thermostat）将每个粒子分别与虚拟热浴耦合。这产生一个很紧密的耦合，好像系统沉浸在一个虚拟的粘性介质中。但是它也以一种显著的方式抑制了自然的动力学。出于此原因，Langevin 调温器（thermostat）应主要被用来产生结构或者系综取样，而不是计算动力学性质。 在 Langevin NVT 模拟中，耦合程度可以用 Friction 参数来设置。它被定义为量纲为时间的倒数，意味着它与 Berendsen 或者 Nose Hoover 温度器（thermostat）的耦合参数的工作方式相反。增加 friction 值会导致与虚拟热浴更紧密的耦合，和对动力学更严格的修正。

在这个部分你将学到如何进行恒定压力下的模拟。

设置一个与 NVT 模拟包含相同模块的脚本（BulkConfiguration, NewCalculator, Optimize ‣ MolecularDynamics）。

打开 MolecularDynamics 设置。通过查看 Type 下面的选项，你会找到两个运行 NPT 模拟的选项：NPT Berendsen 和 NPT Melchionna 算法。

NPT Berendsen 方法的工作原理和 NVT 积分器相同，所以不能精确产生正确的物理系综，尽管偏差通常也很小。而且，QuantumATK 中 Berendsen 的实现只考虑压力标量 $P=1/3(P_{xx}+P_{yy}+P_{zz})$,（其中 $P_{ij}=−σ_{ij}$ 为从应力张量 σ 得到的压力张量的分量），视系统为各项同性。如果模拟像液体或者立方晶体这样的各项同性系统，采用标量压力是一个合适的选择。对于各向异性系统，这个方法无法说明不同方向的不同模量。所以，NPT Berendsen 方法应只能被用于各项同性材料的平衡模拟。

为了将压力分量 $P_{ij}$ 与固定的压力分别耦合，你更应该选择使用 NPT Melchionna 方法⁷⁾。平衡定温定压 1 bar 下的硅超胞的合适的设置如下图所示。

分子动力学（Molecular Dynamics）设置框包含了一般的设置，这些我们现在应该很熟悉。10000 个积分步长足以展示恒压器（barostat）的效果。Log interval 可设置为 50 步以分析涨落。注意这将产生相当大的文件，或许你可以考虑在评估之后删除轨迹文件。

另一个设置框包括恒温器（thermostat）和恒压器（barostat）的设置。恒温器（thermostat）的设置我们已经在之前的部分讨论过。设置External stress 为 1 bar。设置 Barostat time scale 为 100 fs。改变 Bulk modulus 为 98 GPa（硅的文献值）。后面的参数不是特别重要，它只是告诉恒温器（thermostat）体积如何随着应力的变化而改变和确保压力平衡的实际时间标度与所设时间标度的一致性。

最后，应力耦合编组框允许你选择恒压器（barostat）与哪个压力/应力张量分量进行耦合，这意味着系统只与静水压力/应力耦合，而忽视剪切应力分量。这些设置对当前的例子十分有效。

要知道， QuantumATK NPT Melchionna 方法总是将所有压力分量当做互相独立的。并且，不仅是单个外界压力，你也可以为每一个分量设定独立的参考应力值来模拟力学剪切或者蠕变实验。QuantumATK参考手册Reference Manual和例子Simulating a creep experiment of polycrystalline copper 为此功能提供了更详细的解释。

将脚本送到 Editor 来增加一些额外的功能。为了可视化体积和压力随时间变化的涨落，将这几行代码附在脚本的末尾：

# Get the number of snapshots in the trajectory
trajectory_length = md_trajectory.length()
# Extract the cell volume from the trajectory.
volume = [md_trajectory.image(i).bravaisLattice().unitCellVolume().inUnitsOf(Ang**3) for i in range(trajectory_length)]
# Extract the stress
stress = md_trajectory.stresses()
# Calculate the pressure from the negative trace of the stress tensor.
pressure = [-(s[0, 0] + s[1, 1] + s[2, 2]).inUnitsOf(bar)/3.0 for s in stress]
# Extract the simulation time
times = md_trajectory.times().inUnitsOf(ps)
import pylab
# Plot the volume over time.
pylab.figure()
pylab.subplot(2, 1, 1)
pylab.plot(times, volume)
pylab.xlabel('Time (ps)')
pylab.ylabel('Volume (Ang**3)')
pylab.grid(True)
# Plot the pressure over time.
pylab.subplot(2, 1, 2)
pylab.plot(times, pressure)
pylab.xlabel('Time (ps)')
pylab.ylabel('Pressure (bar)')
pylab.grid(True)
pylab.savefig('Fluctuations_NPT_tau100.png')

这几行将从保存的轨迹（trajectory）中的每个快照中提取晶胞体积和应力，并画出其值随模拟时间的变化。

将脚本送到 Job Manager 来进行模拟。这将会花费几分钟来完成。使用 Movie Tool 中的 trajectory 打开轨迹，你就可以监测在模拟过程中晶胞的尺寸和形状的变化。温度在所选的模拟热浴温度300K周围涨落。

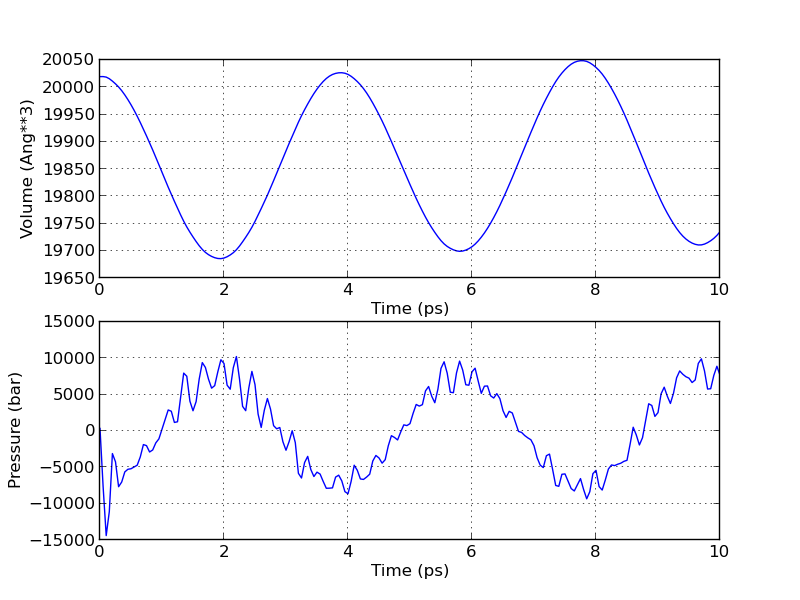
你可以打开 Fluctuations_NPT_tau100.png 来查看体积的涨落。它应该与下图类似。

上面的曲线显示了晶胞体积显著的振荡。这个振荡是 Nose-Hoover 类的温度和压力控制下的典型结果。只要他们的量级保持在合理的范围内，并且在模拟过程中不会急剧增加，那么就没有必要担心。振荡的周期可以通过设置恒压器（Barostat）时间尺度来改变。这个值选的越小，振荡频率越高。振荡的振幅随着恒压器（barostat）时间尺度的减小而增加。

下面的曲线是模拟过程中的压力，显示了类似的行为。它在目标压力 1 bar 附近振荡，但是振幅较大。即时压力值如此大的涨落其实在分子动力学模拟中很正常，因为压力是基于应力来计算的。而应力对于体积变化非常敏感。此外，压力是一个宏观性质，对于如此小的系统考虑相应的平均值比即时值更合理。

NPT 模拟一个典型的应用是模拟相变，比如对石英在不同温度下进行一系列模拟并测量平均晶胞体积随温度变化的函数，来研究α-石英到β-石英相变过程，如文献⁸⁾所报道。

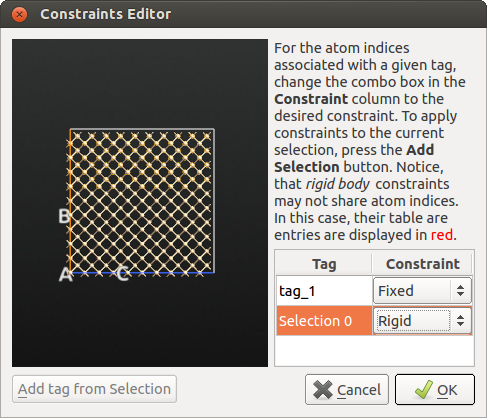
在进行分子动力学模拟过程中你可以固定选中原子的位置。设置这种约束最简单的方式是打开 Molecular Dynamics 工具然后点击 Add constraints 打开 Constraints editor 工具。

在工具栏里你会找到一个表格列出了所有被标签标记的原子组。你可以通过在展示窗口中（用鼠标拖一个矩形或者点住 Ctrl 键选择多个原子）选择所需原子并点击 Add tag from selection 来添加新的原子组。可以在 Constraint 栏中对每一个原子组指定约束条件。第一种将对应原子组里的所有原子固定在它们的初始位置，而第二种将原子组内的原子整体视为一个刚性体。这意味着这些原子根据它们质心所受的力进行协同的移动。在当前的实行中只可能平移运动，而不能进行刚性体旋转。

当使用约束时，你必须注意至少让一个原子保持无约束的。像 NVT NoseHoover 和 NPT Melchionna 这样的恒温器（thermostat）需要至少两个自由原子，因为它们还固定了系统的质心。恒温器（thermostat）会自动适应由约束所导致的自由度数的减少。

然而，你需要知道 Movie Tool 或者 MD Analyzer 中一些功能不能与约束共同使用。比如，当分子动力学模拟中有约束时，Movie Tool 中显示的温度可能不会反应系统自由原子实际的温度，而会显示一个较低温度。你可以通过在脚本里添加动能（kinetic energy）代码来监测温度，如下例所示：

# Get the kinetic energies
kinetic_energies = md_trajectory.kineticEnergies()
# The number of constrained atoms
number_of_constraints = 10
# Calculate the degrees of freedom in the system
degrees_of_freedom = bulk_configuration.numberOfAtoms() - number_of_constraints
# Calculate the temperatures from the kinetic energies
temperatures = [ke/(1.5*degrees_of_freedom)/boltzmann_constant for ke in kinetic_energies]

在 DeviceConfiguration 中实现 NVE/NVT 分子动力学模拟本质上是和在 BulkConfiguration 中一样的方式。拓展到中间区域的电极中的原子自动被约束不动以维持与电极的相容性。虽然技术上可以在 DeviceConfiguration 中实现定压力/应力（NPT）模拟，由于约束的存在，不建议这种计算。对于 DeviceConfiguration 晶胞的优化有多种方法供选择（参见例子Geometry optimization of interfaces）。

• 原文：http://docs.quantumwise.com/tutorials/md_basics.html
• 本文翻译：王吉章